1.CRITIC-TOPSIS法原理
1.1 基本理论
CRITIC-TOPSIS法是一种结合CRITIC(Criteria Importance Through Intercriteria Correlation)法和TOPSIS(Technique for Order Preference by Similarity to Ideal Solution)法的综合评价方法。该方法通过CRITIC法来确定评价指标的权重,再利用TOPSIS法计算各评价对象与理想解和负理想解的接近程度,从而实现对评价对象的排序和优选。这种方法结合了两种方法的优点,既能充分考虑指标之间的冲突性和相关性,又能直观反映评价对象之间的优劣关系。
1.2 CRITIC法原理
CRITIC法是一种客观赋权方法,它根据评价指标的对比强度和指标之间的冲突性来确定指标的权重。具体步骤如下:
- 数据标准化:首先,需要对原始数据进行标准化处理,以消除不同指标之间的量纲差异。标准化公式如下:
其中,是标准化后的数据,
是原始数据,i代表评价对象,j代表评价指标。
2.计算标准差:计算每个评价指标的标准差,以衡量指标的对比强度。标准差越大,说明该指标在不同评价对象之间的差异越大,权重也应相应提高。
其中,m是评价对象的数量,是第j个评价指标的平均值。
3.计算相关系数:计算各评价指标之间的相关系数,以衡量指标之间的冲突性。相关系数绝对值越大,说明两个指标之间的冲突性越小,权重也应相应降低。
4.计算信息量:信息量等于对比强度(标准差)与冲突性(相关系数)的乘积,它综合反映了指标的重要性。
其中,n是评价指标的总数。
5.确定权重:最后,对各评价指标的信息量进行归一化处理,得到各指标的权重。
1.3 TOPSIS法原理
TOPSIS法是一种基于与理想解接近程度进行排序的多属性决策方法。具体步骤如下:
- 构造加权标准化决策矩阵:将标准化后的数据矩阵与CRITIC法确定的权重相乘,得到加权标准化决策矩阵Z。
其中,。
2.确定理想解和负理想解:在加权标准化决策矩阵中,找出每一列的最大值和最小值,分别构成理想解Z+和负理想解Z-。
3.计算距离:计算各评价对象与理想解和负理想解的距离和
。通常采用欧氏距离来计算。
4.计算综合接近度:计算各评价对象的综合接近度,它表示评价对象与理想解的接近程度。
5.排序:根据综合接近度对评价对象进行排序,综合接近度越大的评价对象排名越靠前。
对象进行排序。综合接近度越大的评价对象,其排名越靠前,表示该评价对象在所有评价对象中表现越好。
1.4 CRITIC-TOPSIS法原理
CRITIC-TOPSIS法将CRITIC法和TOPSIS法相结合,首先使用CRITIC法确定各评价指标的权重,然后利用这些权重进行TOPSIS法的计算,从而得到各评价对象的综合排序。
具体步骤如下:
- 数据预处理:对原始数据进行标准化处理,以消除不同指标之间的量纲差异。标准化公式如下:
![]()
其中,xij′是标准化后的数据,xij是原始数据。
2.使用CRITIC法确定权重:按照前面介绍的CRITIC法步骤,计算各评价指标的权重。
3.构造加权标准化决策矩阵:将标准化后的数据xij′与权重wj相乘,得到加权标准化决策矩阵Z。
![]()
4.确定理想解和负理想解:根据加权标准化决策矩阵Z,确定理想解Z+和负理想解Z−。
5.计算距离和综合接近度:按照TOPSIS法的步骤,计算各评价对象与理想解和负理想解的距离和
,以及综合接近度
。
6.排序:根据综合接近度对评价对象进行排序,综合接近度越大的评价对象排名越靠前。
1.5 优缺点分析
CRITIC-TOPSIS法结合了CRITIC法和TOPSIS法的优点,具有以下优点:
- 客观性:CRITIC法基于数据的客观属性确定权重,避免了主观因素的干扰;TOPSIS法则通过计算评价对象与理想解的接近程度进行排序,结果客观可靠。
- 灵活性:该方法可以处理多属性、多指标的评价问题,适用于各种复杂的评价场景。
- 可解释性:通过计算各评价指标的权重,可以清晰地了解各指标在综合评价中的重要性;通过计算综合接近度,可以直观地了解各评价对象的表现。
然而,CRITIC-TOPSIS法也存在一些缺点:
- 敏感性:该方法对原始数据较为敏感,数据的微小变化可能导致结果发生较大变化。
- 权重确定方法:虽然CRITIC法是一种较为客观的权重确定方法,但它仅考虑了数据的客观属性,没有考虑决策者的主观偏好和实际需求。
1.6 结论
CRITIC-TOPSIS法是一种有效的综合评价方法,它结合了CRITIC法和TOPSIS法的优点,能够客观、准确地评价多个对象在不同指标下的表现。在实际应用中,可以根据具体问题和需求选择合适的权重确定方法和排序方法,以获得更加准确和可靠的评价结果。
2.代码
数据集形式:数据与结果都不是绝对的准确,只是用来学习CRITIC-TOPSIS法。
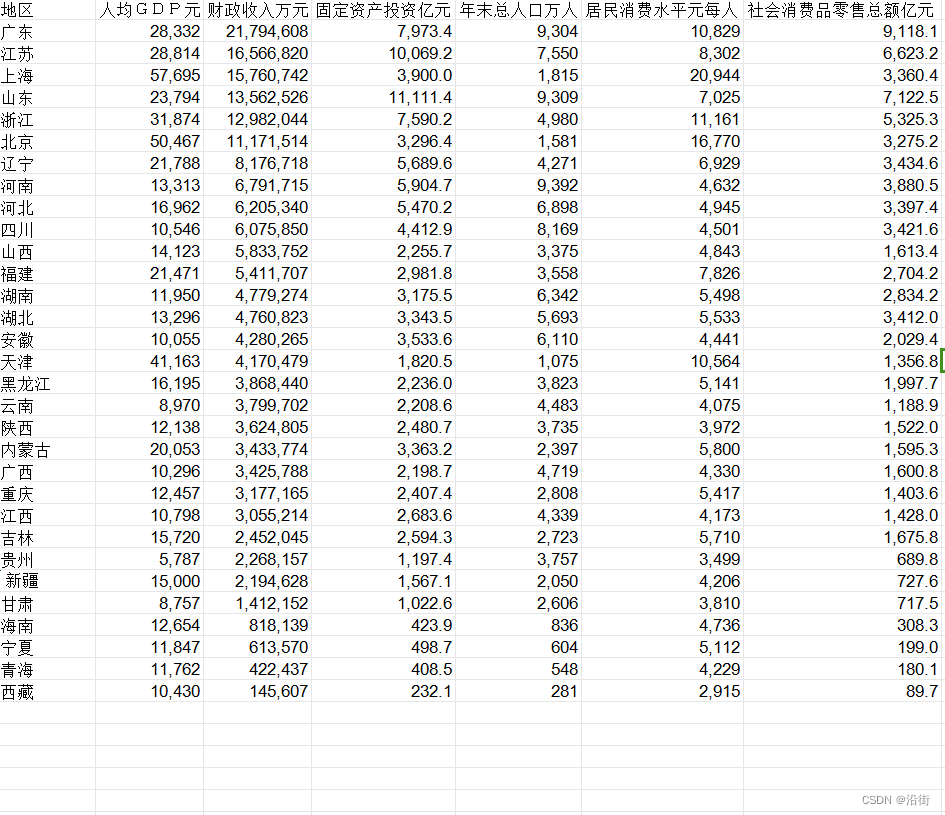
图1
clc;clear;close all;
load('T_25_Jun_2024_19_04_15.mat')
test_data1=G_out_data.test_data1;
zhibiao_label1=ones(1,size(test_data1,2));
zhibiao_label=G_out_data.zhibiao_label; %正向化指标设置
if length(zhibiao_label)<length(zhibiao_label1)
zhibiao_label=[zhibiao_label,zhibiao_label1(length(zhibiao_label)+1:size(test_data1,2))];
end
A_data1=jisuan(test_data1,zhibiao_label); %正向化之后的矩阵
[n,~]=size(A_data1);
A_data =A_data1 ./ repmat(sum(A_data1.*A_data1) .^ 0.5, n, 1); %矩阵归一化
symbol_label=G_out_data.symbol_label; [~,quan]=CRITIC(A_data,symbol_label);
score=TOPSIS(A_data,quan,symbol_label);
disp('CRITIC-TOPSIS法')
disp('评价得分')
score=score'
disp('CRITIC法 得到权重为:')
disp(quan)
Out_table(:,1)=cell2table(G_out_data.table_str);
Out_table(:,2)=array2table(G_out_data.table_data);
Out_table.Properties.VariableNames={'评价对象','评分'};
disp(Out_table) 运行结果如下:数据与结果都不是绝对的准确,只是用来学习CRITIC-TOPSIS法。
| 地区 | 评分 |
| 上海 | 100.00 |
| 广东 | 92.62 |
| 北京 | 87.47 |
| 江苏 | 81.21 |
| 浙江 | 79.42 |
| 山东 | 77.76 |
| 天津 | 58.35 |
| 河南 | 53.08 |
| 辽宁 | 50.43 |
| 河北 | 47.56 |
| 四川 | 45.75 |
| 福建 | 43.13 |
| 湖北 | 39.52 |
| 湖南 | 39.26 |
| 安徽 | 35.10 |
| 内蒙古 | 32.27 |
| 黑龙江 | 30.14 |
| 山西 | 27.93 |
| 吉林 | 27.56 |
| 广西 | 27.34 |
| 江西 | 26.33 |
| 云南 | 25.35 |
| 陕西 | 24.90 |
| 重庆 | 24.53 |
| 新疆 | 18.88 |
| 贵州 | 18.46 |
| 甘肃 | 14.32 |
| 宁夏 | 13.69 |
| 海南 | 13.45 |
| 青海 | 10.59 |
| 西藏 | 6.41 |
简单绘制柱状图如图1所示:
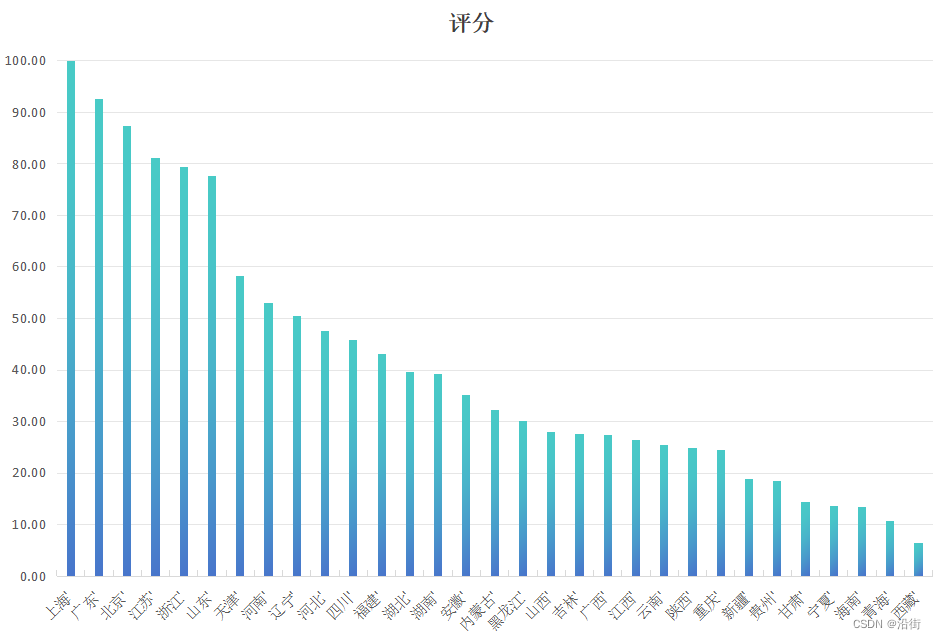
图1 各地区排序







