【机器学习】线性回归

一、问题概述

• 线性：变量之间的关系是一次函数关系，例如直线、平面等。相反，若变量之间的关系不是一次函数关系，称之为非线性。
• 回归：通过有限的条件计算所得的往往是测量值，为了得到真实值，需要进行无限次测量，通过测试数据接近到真实值，这就是回归。

综上，线性回归问题 即通过一个线性模型（一次函数）尽可能准确地预测新样本的输出，通过已知数据预测未知结果。例如：房价预测、电影票房预估等。

1、线性模型

例如：现在有两个变量$x_1、x_2$，假设结果为$h_{\theta }(x)$，则有$$h_{\theta }(x)={\theta }_0+{\theta }_1{x}_1+{\theta }_2{x}_2$$。
其中 ${\theta }_0$ 称为偏置项，${\theta }_1、{\theta }_2$称为权重。

若有$n$个变量，令偏置项 ${\theta }_0$ 的变量值$x_0=1$，则预测值为$$h_{\theta }(x)=\sum _{i=0}^n{\theta }_i{x}_i={\theta }^{T}x$$。

其中 $\theta =[{\theta }_0,{\theta }_1,{\theta }_2]$ 为一个行矩阵。

2、误差损失

假设一个线性模型：

可以看出预测值与真实值之间并不是完全对等的，因此引入误差 $\epsilon$。

对于每个样本：$y^{(i)}={\theta }^T{x}^{(i)}+{\epsilon }^{(i)}$。${\epsilon }^{(i)}$称为误差项，不同样本的误差项也不一定相同。

误差 ${\epsilon }^{(i)}$ 符合独立同分布并且服从均值为$0$、方差为${\theta }^2$的高斯分布（正态分布）。

3、似然函数

由于误差服从高斯分布，则有：
$$p({\epsilon }^{(i)})=\frac{1}{\sqrt{2\pi \sigma }}\exp (-\frac{({\epsilon }^{(i)}{)}^2}{2{\sigma }^2})$$
将 $y^{(i)}={\theta }^T{x}^{(i)}+{\epsilon }^{(i)}$ 代入得到：
$$p(y^{(i)}|x^{(i)};\theta )=\frac{1}{\sqrt{2\pi \sigma }}\exp (-\frac{(y^{(i)}-{\theta }^T{x}^{(i)}{)}^2}{2{\sigma }^2})$$
因此 似然函数 为：
$$L(\theta )=\prod _{i=1}^{m}p(y^{(i)}|x^{(i)};\theta )=\prod _{i=1}^m\frac{1}{\sqrt{2\pi \sigma }}\exp (-\frac{(y^{(i)}-{\theta }^T{x}^{(i)}{)}^2}{2{\sigma }^2})$$
转化为对数似然：
$$\begin{array}{rl}\ln L(\theta )& =\sum _{i=1}^m\ln \frac{1}{\sqrt{2\pi \sigma }}\exp (-\frac{(y^{(i)}-{\theta }^T{x}^{(i)}{)}^2}{2{\sigma }^2})\\ & =m\ln \frac{1}{\sqrt{2\pi \sigma }}-\frac{1}{{\sigma }^2}\cdot \frac{1}{2}\sum _{i=1}^m(y^{(i)}-{\theta }^T{x}^{(i)}{)}^2\end{array}$$
令
$$J(\theta )=\frac{1}{2}\sum _{i=1}^m(y^{(i)}-{\theta }^T{x}^{(i)}{)}^2（最小二乘法）$$
$J(\theta )$即损失函数 ，由于似然函数来源于高斯分布，则应使似然函数越大越好，即 $J(\theta )$越小越好。

怎么让$J(\theta )$取得最小值呢？——求导：

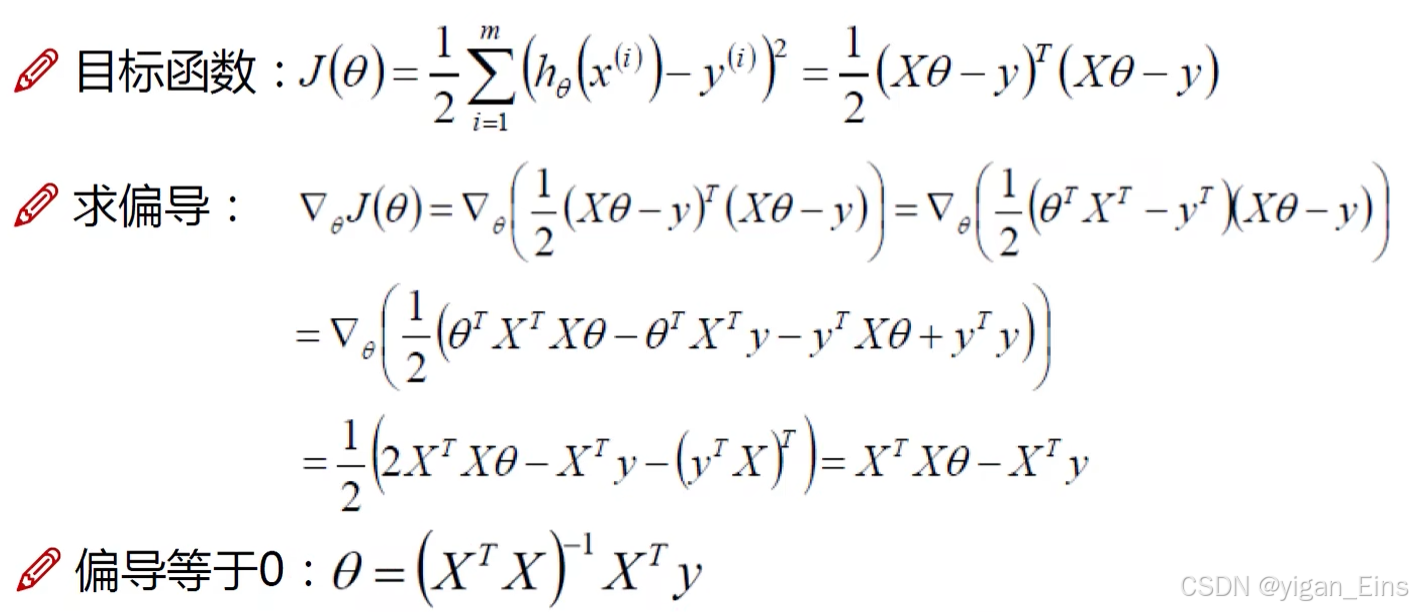
注：这一部分不需要掌握，当时需要理解。

4、梯度下降

对于最小值的求解问题，我们可以将其近似看做一个小山，那么局部最小值就变成了下山问题：

由于 梯度（切线）方向总是下降的，因此我们每次沿着梯度方向前进一小步逼近局部最优解的过程，即称为 梯度下降。

那步长怎么取呢？
  对于最优解的求解，我们的惯性思维自然是越快越好，即将步长设置成一个较大值，一般情况下可以很快的逼近局部最优解。但是，如果在一个逼近局部最优解的小区间，由于步长较大，求解过程可能在最优解附近反复横跳，将永远不会收敛，即永远取不到局部最优解。因此，我们的步长不应取得很大，也不宜取得很小，因此如果步长过小，逼近局部最优解得过程将会很慢，时间利用率不高。

由于权值及偏置项之间是独立的，因此我们分开求解：
对于一个 ${\theta }_j$，我们关于$J(\theta )$对其求偏导并取平均:
$$\frac{\partial J(\theta )}{\partial {\theta }_j}=-\frac{1}{m}\sum _{i=1}^m(y^i-h_{\theta }(x^i))x_j^i$$
而梯度是下降的，因此我们取步长 $\frac{1}{m}{\sum }_{i=1}^m(y^i-h_{\theta }(x^i))x_j^i$，则：
$${\theta }_j^{\prime }={\theta }_j+\frac{1}{m}\sum _{i=1}^m(y^i-h_{\theta }(x^i))x_j^i$$
这样虽然能比较容易地取得最优解，但是对于每个权重地每次更新，我们都考虑对所有样本进行计算，在权重数多或样本量大的情况下，梯度下降会非常缓慢。因此，我们考虑每次随机地选择一个样本进行更新：$${\theta }_j^{\prime }={\theta }_j+\frac{1}{batch}\sum _{i=1}^{batch}(y^i-h_{\theta }(x^i))x_j^i$$
这就是 随机梯度下降 。

但是新的问题随之而来，如果存在恶意样本，那么选择这个样本的时候可能会破坏原本的梯度下降，产生副作用。因此，我们考虑将全部样本集划分为小批量样本集，每次选择一个小批量数据集进行更新，即避免了样本量大导致的缓慢，又减少了恶意样本带来的破坏。

如果每次都这样进行更新，则样本量确定的情况下，步长也确定了，这似乎不太美妙，我们在训练的过程中更多的希望能自行控制步长，而不是完全依赖样本量，因此，我们在计算步长时引入 学习率 ，控制训练过程中的步长：$${\theta }_j^{\prime }={\theta }_j+\alpha \cdot \frac{1}{batch}\sum _{i=1}^{batch}(y^i-h_{\theta }(x^i))x_j^i$$

这就是 梯度下降更新参数 的方法。

二、算法实现

  上一阶段我们已经了解线性模型，损失函数以及梯度下降的步骤，这一阶段将使用python实现线性回归算法。

首先我们需要一些对数据集进行预处理的方法，主要作用是对数据集进行标准化和归一化，ML_algorithm包已上传百度网盘

链接: https://pan.baidu.com/s/12CsQM8CILOrHnS0rQQOYYw?pwd=6666 
提取码: 6666

1、 定义 LinearRegression 类，并在__init__函数中进行初始化，$self.theta$ 即为参数矩阵，初始化为一个值为0的列向量。

2、 在 train 方法中对线性模型进行训练，执行梯度下降更新参数矩阵。

3、 在 gradient_descent 函数中进行迭代，在 gradient_step 中进行梯度计算，即使用上一阶段得到的梯度下降更新参数的方法 更新参数矩阵 。

4、 在 loss_function 中进行损失计算，即 利用 $J(\theta )$ 计算损失 ，在计算中，由于我们使用矩阵进行计算，求得的是所有样本的损失和。因此，需要除以样本量，取平均值 。

🍁 线性回归算法完整代码：

import numpy as np
from ML_algorithm.utils.features.prepare_for_training import prepare_for_trainingclass LinearRegression:def __init__(self,data,labels,polynomial_degree = 0,sinusoid_degree = 0,normalize_data = True):"""1.对数据进行预处理2.先得到所有的特征个数3.初始化参数矩阵"""(data_processed,features_mean,features_deviation) = prepare_for_training(data,polynomial_degree,sinusoid_degree,normalize_data)self.data = data_processedself.labels = labelsself.features_mean = features_meanself.features_deviation = features_deviationself.polynomial_degree = polynomial_degreeself.sinusoid_degree = sinusoid_degreeself.normalize_data = normalize_datanum_features = self.data.shape[1] # 数据的特征个数self.theta = np.zeros((num_features,1)) # 初始化参数矩阵为一个初始值为0的num_features行1列的矩阵def train(self,alpha,num_iterations = 500):loss_list = self.gradient_descent(alpha,num_iterations)return self.theta,loss_listdef gradient_descent(self,alpha,num_iterations):"""梯度下降返回一个损失矩阵alpha : 学习率num_iterations : 迭代次数"""loss_history = []for _ in range(num_iterations):self.gradient_step(alpha)loss_history.append(self.loss_function(self.data,self.labels))return loss_historydef gradient_step(self,alpha):"""梯度下降参数更新计算方法，注意是矩阵运算"""num_examples = self.data.shape[0]prediction = LinearRegression.hypothesis(self.data,self.theta)delta = self.labels - predictiontheta = self.thetatheta = theta + alpha * (1 / num_examples) * (np.dot(delta.T,self.data)).T # 将循环累加转化为矩阵点乘，更新thetaself.theta = thetadef loss_function(self,data,labels):"""损失计算"""num_examples = data.shape[0]delta = labels - LinearRegression.hypothesis(self.data,self.theta)loss = (1 / 2) * np.dot(delta.T,delta) / num_examples # 取平均值return loss[0][0]@staticmethoddef hypothesis(data,theta):"""预测值计算"""predictions = np.dot(data,theta)return predictionsdef get_loss(self,data,labels):data_processed = prepare_for_training(data,self.polynomial_degree,self.sinusoid_degree,self.normalize_data)[0]return self.loss_function(data_processed,labels)def get_prediction(self,data):"""用训练的参数模型，预测得到回归值结果"""data_processed = prepare_for_training(data,self.polynomial_degree,self.sinusoid_degree,self.normalize_data)[0]predictions = LinearRegression.hypothesis(data_processed,self.theta)

三、应用实例

  这一阶段，我们要将理论部分和实现的算法进行实战。

在ML_algorithm包中提供了数据集world-happiness-report-2017.csv，我们将利用这一数据集进行实战。

1、 首先，使用 read_csv 方法读取数据集，再用 .sample 方法对数据集进行切割，分成训练集和测试集。

2、 然后，对训练集和测试集进行分离，获得变量和结果对应的 向量。

绘制数据分布散点图：

3、 接着，导入 LinearRegression 类， 使用训练集对线性模型进行训练 。

绘制损失函数折线图：

4、 最后，对线性模型进行测试。

线性方程折线图：

可以看出：得到的线性模型能够较准确地吻合数据分布。

🍁 实战完整代码：

import numpy as np
import pandas as pd
import matplotlib.pyplot as pltfrom linear_regression import LinearRegression# 数据集处理部分
dataset = pd.read_csv('ML_algorithm/data/world-happiness-report-2017.csv')train_data = dataset.sample(frac = 0.8) # 训练集
test_data = dataset.drop(train_data.index) # 测试集input_param_name = 'Economy..GDP.per.Capita.'
output_param_name = 'Happiness.Score'x_train = train_data[[input_param_name]].values
y_train = train_data[[output_param_name]].valuesx_test = test_data[input_param_name].values
y_test = test_data[output_param_name].valuesplt.scatter(x_train,y_train,label = 'Train data') # scatter绘制散点图，数据1
plt.scatter(x_test,y_test,label = 'Test data') # 数据2
plt.xlabel(input_param_name) # x轴
plt.ylabel(output_param_name) # y轴
plt.title('Happy') # 图名
plt.legend()
plt.show()# 训练部分
num_iterations = 500 # 迭代轮次
learning_rate = 0.01 # 学习率linear_regression = LinearRegression(x_train,y_train)
(theta,loss) = linear_regression.train(learning_rate,num_iterations)print('开始时的损失',loss[0])
print('训练后的损失',loss[-1])plt.plot(range(num_iterations),loss) # plot绘制折线图
plt.xlabel('Iter')
plt.ylabel('loss')
plt.title('GD')
plt.show()# 测试部分
predictions_num = 100
x_precitions = np.linspace(x_train.min(),x_train.max(),predictions_num).reshape(predictions_num,1)
y_precitions = linear_regression.get_prediction(x_precitions)plt.scatter(x_train,y_train,label = 'Train data') # scatter绘制散点图，数据1
plt.scatter(x_test,y_test,label = 'Test data') # 数据2
plt.plot(x_precitions,y_precitions,'r',label = 'Prediction')
plt.xlabel(input_param_name) # x轴
plt.ylabel(output_param_name) # y轴
plt.title('Happy') # 图名
plt.legend()
plt.show()