对于低频信号,阻容耦合电路中的阻容耦合电容对于低频信号是有抑制的
对于高频信号,三极管中的结电容(极间电容)对其是有抑制的
幅频特性与相频特性
频率响应研究的就是放大倍数与频率之间的关系,只有在一定的频率范围之内电路的放大倍数才不会收到影响,实际过程之中,我们观察到f与Au的变化范围都非常的广,因此对于横坐标f我们通常取lg,而对于纵坐标的放大倍数我们取20lgAu,以便于我们观察到更多的信号
这个经过我们升级的图就叫做波特图
通频带:放大倍数下降3db之间的频率,分别叫做下限截止频率与上限截止频率
一般来讲多级放大电路电路的通频带会比单级放大电路更窄
当我们改善电路的放大倍数的时候,通频带肯定会减小
当我们改善通频带的时候,放大倍数也会减小,这是两个普遍规律,毕竟鱼与熊掌不可兼得
|Au| = F(f)增益与频率之间的关系
= F(f) 相位与频率之间的关系
高通电路
也即是对于高频信号,信号几乎无损失的通过,低频,电容的容抗不容忽略,信号将在其上产生压降,从而产生干扰
公式推导





大于零表示超前相移,
小于零表示滞后相移
低通电路
对于低频信号几乎无损耗的通过,对于高频信号却存在损失
公式推导





波特图



混合π等效模型
考虑了之前H等效模型在低频信号下所忽略的结电容,在H参数等效模型上加入了集电结电容u与发射结电容
π


主要参数
低频段(无相移)参数
电流放大系数o,电压放大倍数K =
ce /
be
bb,与
be从手册中可查,
be = (1+
)
T/
EQ
π模型的推导



在以前我们所讨论的放大倍数是在集电极与发射级之间的电压在一个固定的条件之下讨论的,但是现在出现了变化因为有了π
的存在导致我们输入的信号必然会产生相位的偏移与大小的改变,所以这个放大倍数是一个向量而不是一个固定的值
单管共射的分析
先中频段再低频段后高频段
先用直流再算交流,用T计算
π
π
不过是中间的过程而已,因为
π
是等效出来的的值,就会受到环境的影响
在求解高频的响应之中我们应该求解出π然后在中频段求解出来的
u
的值进行代入求解,因为在高频段求解
u
是困难的
总结:低频段求出π , 中频段求出K , 高频带入低中频求出来的数据,推出近似的高频段的
π
放到高频之中
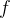 L与
L与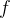 H的计算
H的计算
计算从电容C看过去的戴维南等效电路然后直接计算L与
H,如下图


高频时计算过程是从π
看进去的戴维南等效电路计算电阻

中频段的Aus---->Ausm,bw--->中频带,
bw =
H-
L

上面的增益与通频的乘积我们将他叫做增益带宽积,显然要得到更好的增益带宽积,我们可以使用u
更小的晶体管
多级放大电路的频率响应
频率与相移
对于低频来讲,耦合电容有两个的时候,晶体管只有一个的时候,此时在低频的增益会出现40lg
对于高频来讲,耦合电容有一个的时候,晶体管有两个的时候,此时在高频的增益会出现40lg
Cπ(等效结电容)影响高频,而C(耦合电容)影响低频,所以Cπ
有两个,具体表现为晶体管有两个时,高频增益为20lg,而对于C来讲,当C有两个时,低频的增益就为40lg!!!!
而对于相移来讲
相移就是输入与输出的相位之差 , 对于三级的放大电路来讲,相移最大为-270度

精确定位问题求解全过程文档及程序)





