代码随想录Day 58|拓扑排序、dijkstra算法精讲，题目:软件构建、参加科学大会

提示：DDU，供自己复习使用。欢迎大家前来讨论~

图论part08

拓扑排序精讲

题目：117. 软件构建

117. 软件构建 (kamacoder.com)

拓扑排序的背景

拓扑排序：

1. 图论问题：拓扑排序是图论中的一个经典问题。
2. 应用场景：
   • 大学排课：需要按照先决条件排序课程。
   • 文件处理：在项目安装或依赖管理中处理复杂的文件依赖关系。
3. 处理大规模依赖：适用于处理成千上万的依赖关系。
4. 检测循环依赖：拓扑排序可以发现循环依赖，即无法进行线性排序的情况。
5. 排序目标：将有向图中的顶点转换为线性顺序。

解题思路：

1. 广度优先搜索（BFS）：这是实现拓扑排序最常用的方法，简单易懂。
2. 算法步骤：
   • 入度表：首先构建一个入度表，记录每个顶点的入度，即指向该顶点的边的数量。
   • 队列：将所有入度为0的顶点（即没有任何顶点指向的顶点）加入队列。
   • 处理队列：当队列非空时，依次从队列中取出一个顶点，加入到拓扑排序的结果序列中，并减少与该顶点相邻的顶点的入度。如果相邻顶点的入度变为0，也将它们加入队列。
   • 重复：重复上述过程，直到队列为空。
   • 检测环：如果结果序列中的顶点数小于图中顶点的总数，说明图中存在环，无法进行拓扑排序。
3. 深度优先搜索（DFS）：另一种实现拓扑排序的方法，但不是本篇的重点。
4. 卡恩算法：1962年提出的拓扑排序算法，基于BFS。
5. 核心思想：拓扑排序的核心思想是将有向无环图中的顶点进行线性排序，同时检测图中是否存在环。

拓扑排序的简单理解：

1. 找起点：先找到所有没有任何前置条件（入度为0）的节点。

2. 加入结果：把这些节点加入到一个结果列表中。

3. 移除节点：从图中删除这些节点，以及它们指向的所有边。

4. 重复：重复以上步骤，直到找不到入度为0的节点。

5. 检测环：如果最后结果列表中的节点数和图中的节点数不一样，说明有环，无法完成排序。

6. 输出：如果能找到完整的排序，就输出结果列表；否则，说明存在环，输出错误信息。

拓扑排序就是按照一定的顺序，把图中的节点排成一行，同时确保所有的依赖关系都得到满足。如果排不出这样的顺序，就说明图中有环，存在无法解决的依赖关系。

模拟过程

假设我们有以下的任务依赖关系：

A -> C
A -> D
B -> C
C -> D

这意味着：

• 要执行任务C，必须先执行任务A。
• 要执行任务D，必须先执行任务A和C。
• 要执行任务C，必须先执行任务B。

我们来模拟拓扑排序的步骤：

步骤1：初始化

• 入度：A=0, B=0, C=2（A->C, B->C）, D=2（A->D, C->D）
• 依赖关系：A->(C, D), B->©, C->(D)
• 结果集：()

步骤2：找到入度为0的节点

• A和B的入度都为0，我们可以选择A或B作为起点。这里我们选择A。

步骤3：加入结果集并移除节点

• 结果集变为：(A)
• 移除A及其依赖关系，更新入度：
  • 移除A后，C的入度变为1（只剩B->C），D的入度变为1（只剩C->D）。

步骤4：重复步骤2

• 接下来，我们再次找入度为0的节点，现在B的入度为0。

步骤5：加入结果集并移除节点

• 结果集变为：(A, B)
• 移除B及其依赖关系，更新入度：
  • 移除B后，C的入度变为0。

步骤6：重复步骤2

• 现在C的入度为0。

步骤7：加入结果集并移除节点

• 结果集变为：(A, B, C)
• 移除C及其依赖关系，更新入度：
  • 移除C后，D的入度变为0。

步骤8：重复步骤2

• 最后，D的入度为0。

步骤9：加入结果集

• 结果集变为：(A, B, C, D)

步骤10：检测环

• 结果集的节点数等于图中的节点数，说明没有环，我们可以完成排序。

最终结果：(A, B, C, D)

这个顺序告诉我们，为了满足所有依赖关系，我们可以先执行A，然后执行B，接着执行C，最后执行D。

如果在这个过程中，我们发现无法再找到入度为0的节点，但结果集中的节点数小于图中节点的总数，那么我们可以确定图中存在环，无法进行拓扑排序。

最后代码如下：

#include <iostream>
#include <vector>
#include <queue>
#include <unordered_map>
using namespace std;
int main() {int m, n, s, t;cin >> n >> m;vector<int> inDegree(n, 0); // 记录每个文件的入度unordered_map<int, vector<int>> umap;// 记录文件依赖关系vector<int> result; // 记录结果while (m--) {// s->t，先有s才能有tcin >> s >> t;inDegree[t]++; // t的入度加一umap[s].push_back(t); // 记录s指向哪些文件}queue<int> que;for (int i = 0; i < n; i++) {// 入度为0的文件，可以作为开头，先加入队列if (inDegree[i] == 0) que.push(i);//cout << inDegree[i] << endl;}// int count = 0;while (que.size()) {int  cur = que.front(); // 当前选中的文件que.pop();//count++;result.push_back(cur);vector<int> files = umap[cur]; //获取该文件指向的文件if (files.size()) { // cur有后续文件for (int i = 0; i < files.size(); i++) {inDegree[files[i]] --; // cur的指向的文件入度-1if(inDegree[files[i]] == 0) que.push(files[i]);}}}if (result.size() == n) {for (int i = 0; i < n - 1; i++) cout << result[i] << " ";cout << result[n - 1];} else cout << -1 << endl;}

dijkstra（朴素版）精讲

题目：47. 参加科学大会

[47. 参加科学大会（第六期模拟笔试） (kamacoder.com)](https://kamacoder.com/problempage.php?pid=1053)

解题思路

1. 最短路径问题：在有向图中，给定一个起点和一个终点，求出从起点到终点的最短路径。
2. Dijkstra算法：一种用于在有权图中找到从单个源点到所有其他节点的最短路径的算法。这里的权值是非负数。
3. Dijkstra算法的特点：
   • 可以同时求出源点到所有其他节点的最短路径。
   • 权值不能为负数。
4. 算法思路：Dijkstra算法采用贪心策略，不断寻找距离源点最近的未访问节点。
5. Dijkstra算法的三部曲：
   • 第一步：选择源点到最近且未被访问过的节点。
   • 第二步：将这个最近节点标记为已访问。
   • 第三步：更新非访问节点到源点的距离。
6. 与Prim算法的比较：Dijkstra算法和Prim算法在思路上非常相似，都是贪心算法，但Prim算法用于最小生成树问题。
7. minDist数组：在Dijkstra算法中，minDist数组用于记录每个节点到源点的最小距离，这是理解算法的核心。
8. 算法演示：通过画图的方式展示了Dijkstra算法的工作过程，帮助理解算法是如何逐步找到最短路径的。

朴素版dijkstra

模拟过程

---

0、初始化

minDist数组数值初始化为int最大值。

这里在强点一下 minDist数组的含义：记录所有节点到源点的最短路径，那么初始化的时候就应该初始为最大值，这样才能在后续出现最短路径的时候及时更新。

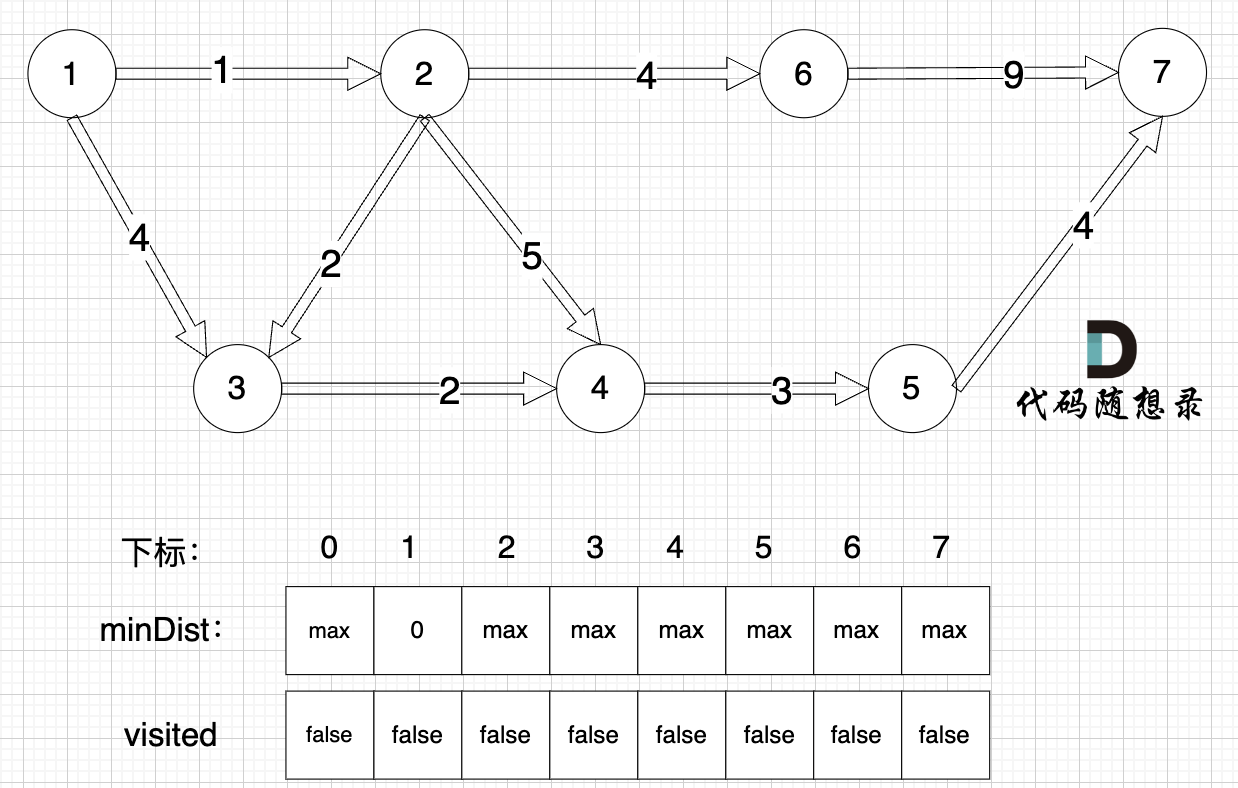
（图中，max 表示默认值，节点0 不做处理，统一从下标1 开始计算，这样下标和节点数值统一， 方便大家理解，避免搞混）

源点（节点1） 到自己的距离为0，所以 minDist[1] = 0

此时所有节点都没有被访问过，所以 visited数组都为0

---

以下为dijkstra 三部曲

1、选源点到哪个节点近且该节点未被访问过

源点距离源点最近，距离为0，且未被访问。

2、该最近节点被标记访问过

标记源点访问过

3、更新非访问节点到源点的距离（即更新minDist数组） ，如图：

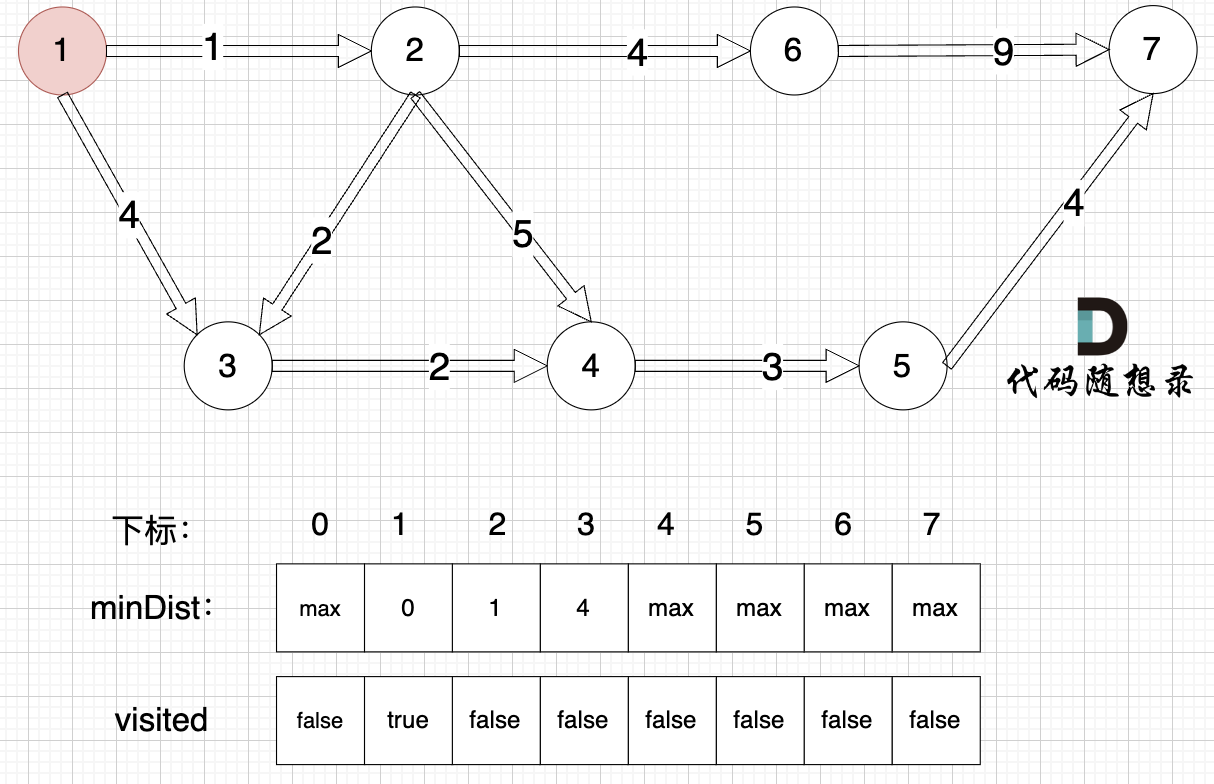
更新 minDist数组，即：源点（节点1） 到 节点2 和 节点3的距离。

• 源点到节点2的最短距离为1，小于原minDist[2]的数值max，更新minDist[2] = 1
• 源点到节点3的最短距离为4，小于原minDist[3]的数值max，更新minDist[3] = 4

可能有录友问：为啥和 minDist[2] 比较？

再强调一下 minDist[2] 的含义，它表示源点到节点2的最短距离，那么目前我们得到了 源点到节点2的最短距离为1，小于默认值max，所以更新。 minDist[3]的更新同理

---

1、选源点到哪个节点近且该节点未被访问过

未访问过的节点中，源点到节点2距离最近，选节点2

2、该最近节点被标记访问过

节点2被标记访问过

3、更新非访问节点到源点的距离（即更新minDist数组） ，如图：

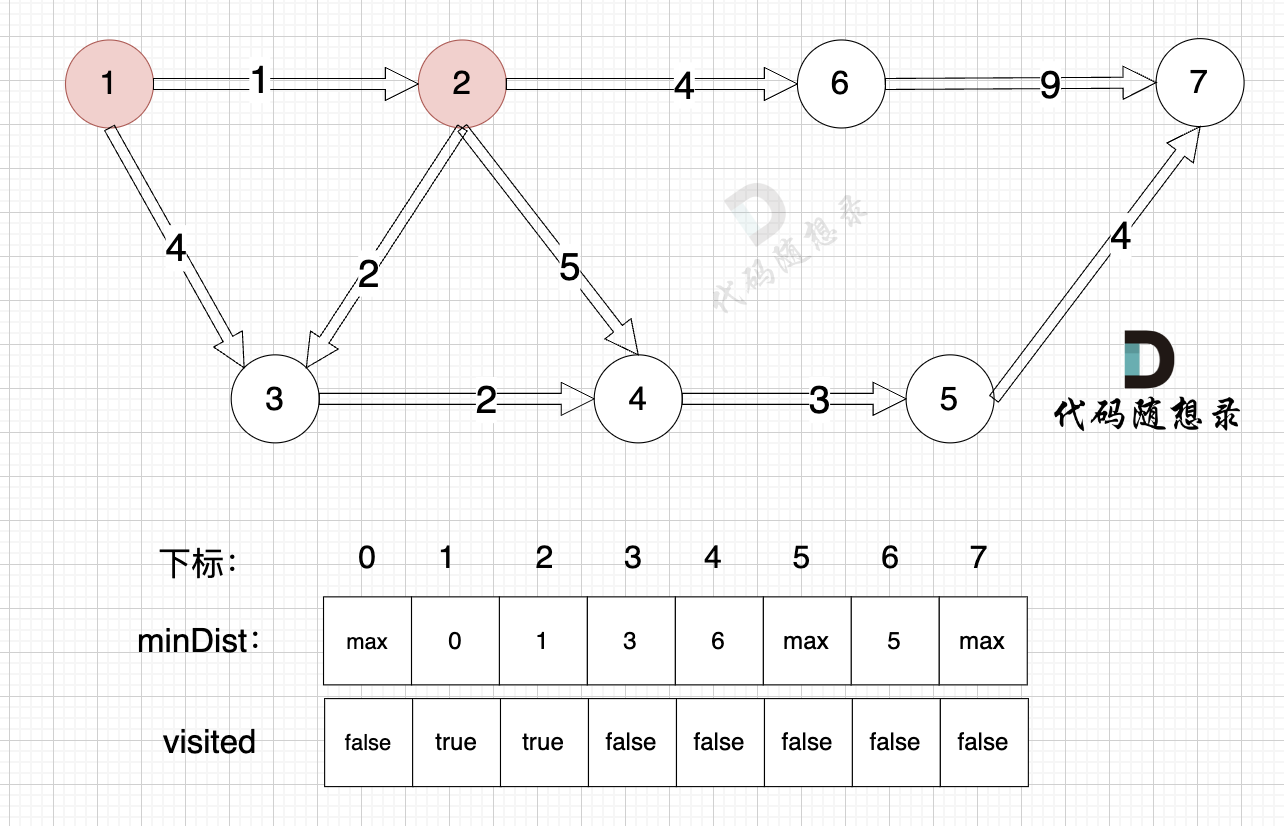
更新 minDist数组，即：源点（节点1） 到 节点6 、 节点3 和 节点4的距离。

为什么更新这些节点呢？ 怎么不更新其他节点呢？

因为 源点（节点1）通过 已经计算过的节点（节点2） 可以链接到的节点 有 节点3，节点4和节点6.

更新 minDist数组：

• 源点到节点6的最短距离为5，小于原minDist[6]的数值max，更新minDist[6] = 5
• 源点到节点3的最短距离为3，小于原minDist[3]的数值4，更新minDist[3] = 3
• 源点到节点4的最短距离为6，小于原minDist[4]的数值max，更新minDist[4] = 6

---

1、选源点到哪个节点近且该节点未被访问过

未访问过的节点中，源点距离哪些节点最近，怎么算的？

其实就是看 minDist数组里的数值，minDist 记录了 源点到所有节点的最近距离，结合visited数组筛选出未访问的节点就好。

从 上面的图，或者 从minDist数组中，我们都能看出 未访问过的节点中，源点（节点1）到节点3距离最近。

2、该最近节点被标记访问过

节点3被标记访问过

3、更新非访问节点到源点的距离（即更新minDist数组） ，如图：

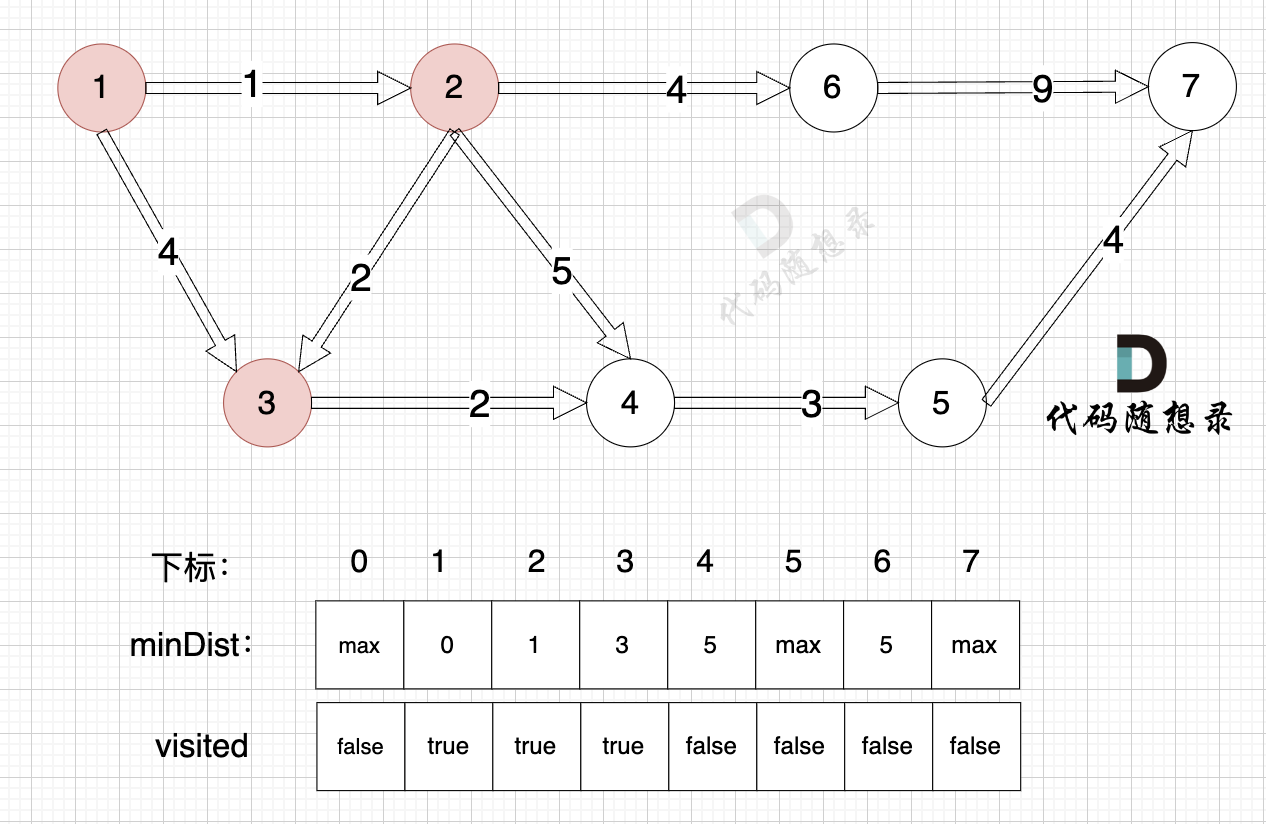
由于节点3的加入，那么源点可以有新的路径链接到节点4 所以更新minDist数组：

更新 minDist数组：

• 源点到节点4的最短距离为5，小于原minDist[4]的数值6，更新minDist[4] = 5

---

1、选源点到哪个节点近且该节点未被访问过

距离源点最近且没有被访问过的节点，有节点4 和 节点6，距离源点距离都是 5 （minDist[4] = 5，minDist[6] = 5） ，选哪个节点都可以。

2、该最近节点被标记访问过

节点4被标记访问过

3、更新非访问节点到源点的距离（即更新minDist数组） ，如图：

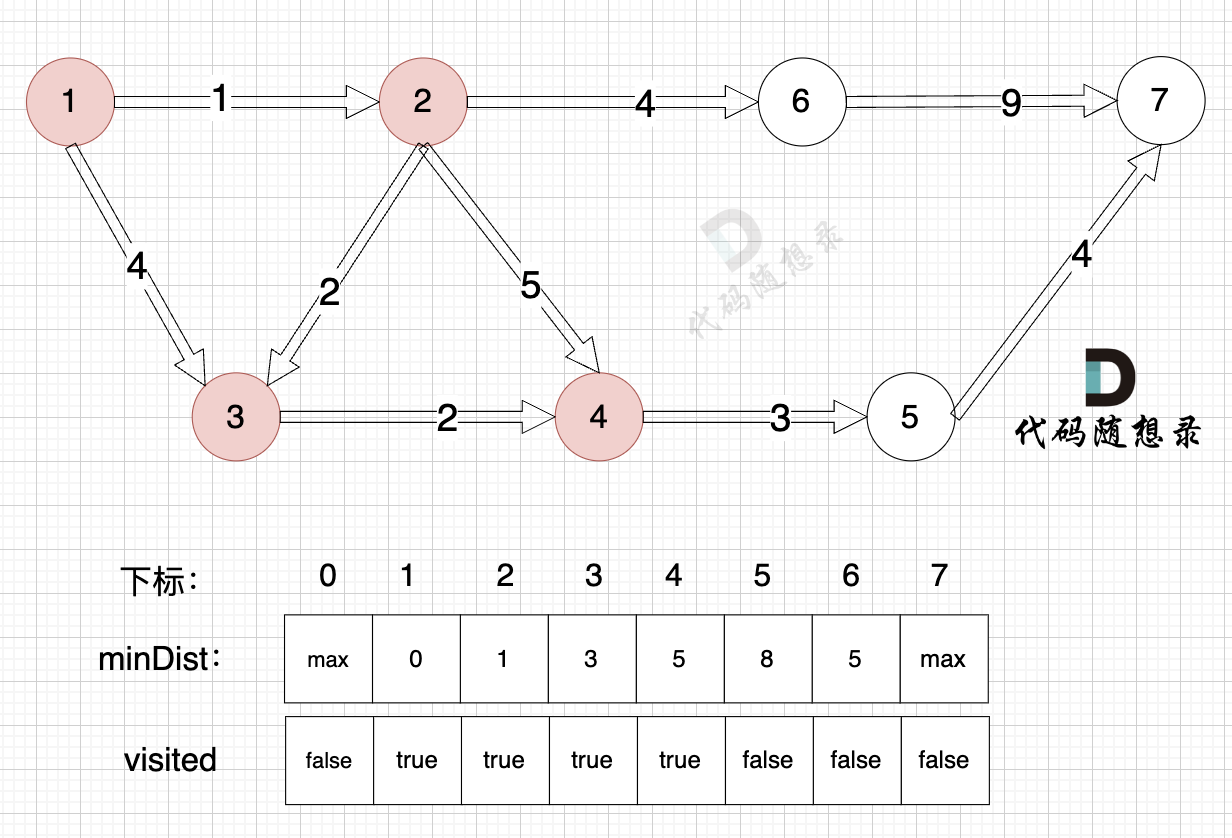
由于节点4的加入，那么源点可以链接到节点5 所以更新minDist数组：

• 源点到节点5的最短距离为8，小于原minDist[5]的数值max，更新minDist[5] = 8

---

1、选源点到哪个节点近且该节点未被访问过

距离源点最近且没有被访问过的节点，是节点6，距离源点距离是 5 （minDist[6] = 5）

2、该最近节点被标记访问过

节点6 被标记访问过

3、更新非访问节点到源点的距离（即更新minDist数组） ，如图：

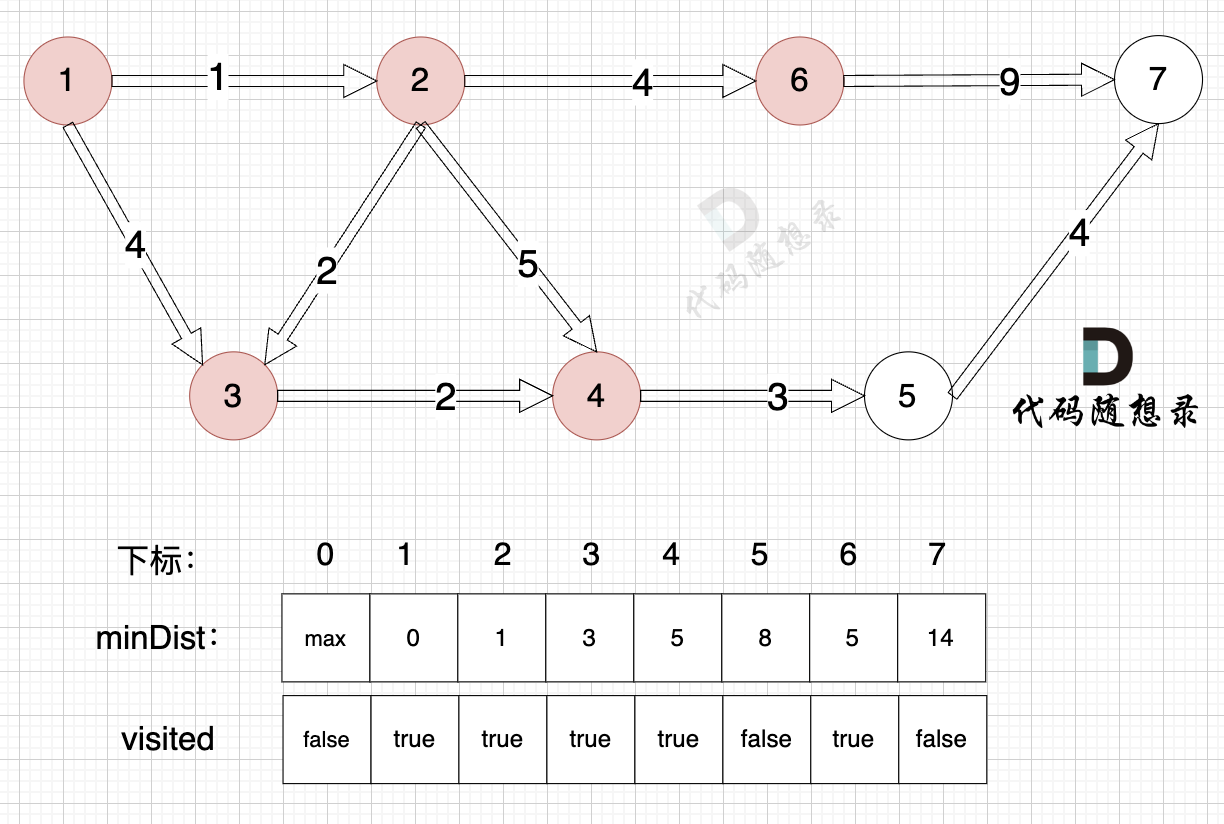
由于节点6的加入，那么源点可以链接到节点7 所以 更新minDist数组：

• 源点到节点7的最短距离为14，小于原minDist[7]的数值max，更新minDist[7] = 14

---

1、选源点到哪个节点近且该节点未被访问过

距离源点最近且没有被访问过的节点，是节点5，距离源点距离是 8 （minDist[5] = 8）

2、该最近节点被标记访问过

节点5 被标记访问过

3、更新非访问节点到源点的距离（即更新minDist数组） ，如图：

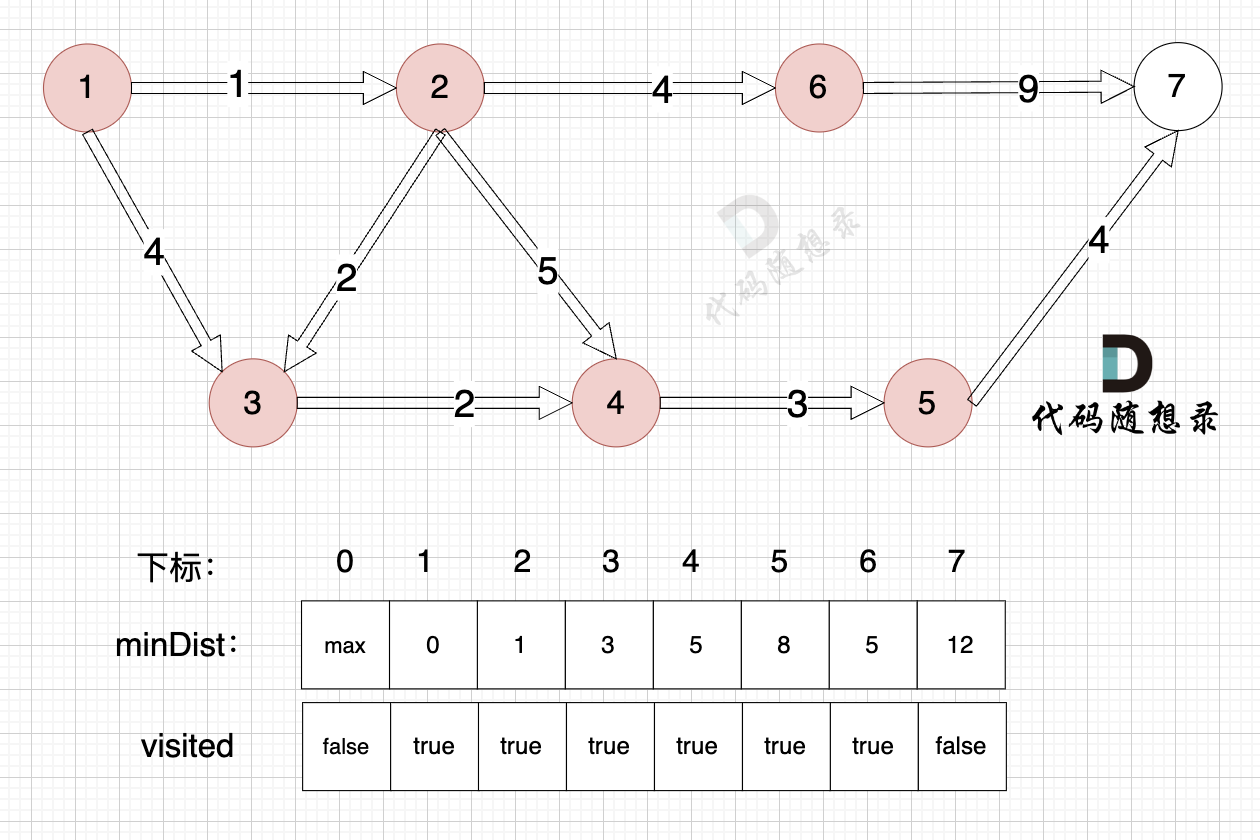
由于节点5的加入，那么源点有新的路径可以链接到节点7 所以 更新minDist数组：

• 源点到节点7的最短距离为12，小于原minDist[7]的数值14，更新minDist[7] = 12

---

1、选源点到哪个节点近且该节点未被访问过

距离源点最近且没有被访问过的节点，是节点7（终点），距离源点距离是 12 （minDist[7] = 12）

2、该最近节点被标记访问过

节点7 被标记访问过

3、更新非访问节点到源点的距离（即更新minDist数组） ，如图：

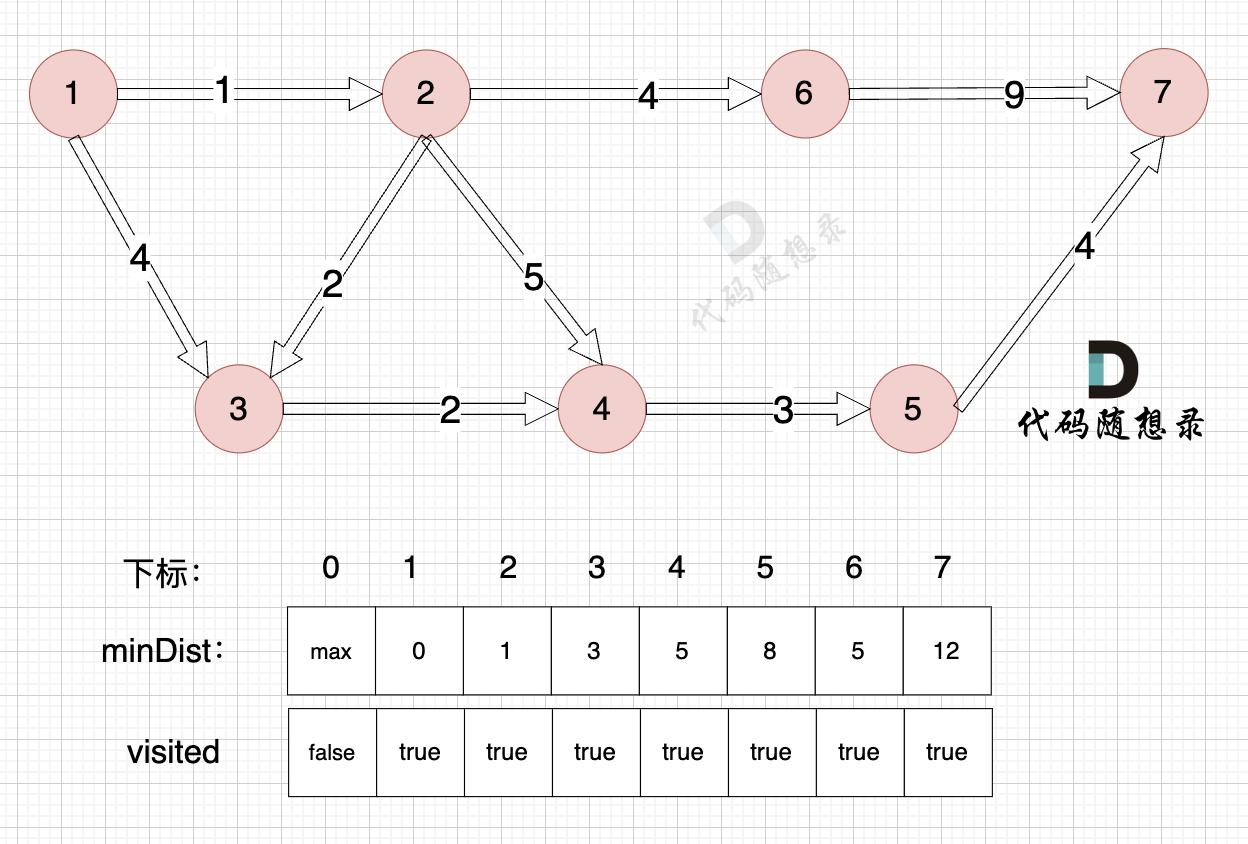
节点7加入，但节点7到节点7的距离为0，所以 不用更新minDist数组

---

最后我们要求起点（节点1） 到终点 （节点7）的距离。

再来回顾一下minDist数组的含义：记录 每一个节点距离源点的最小距离。

那么起到（节点1）到终点（节点7）的最短距离就是 minDist[7] ，按上面举例讲解来说，minDist[7] = 12，节点1 到节点7的最短路径为 12。

路径如图：

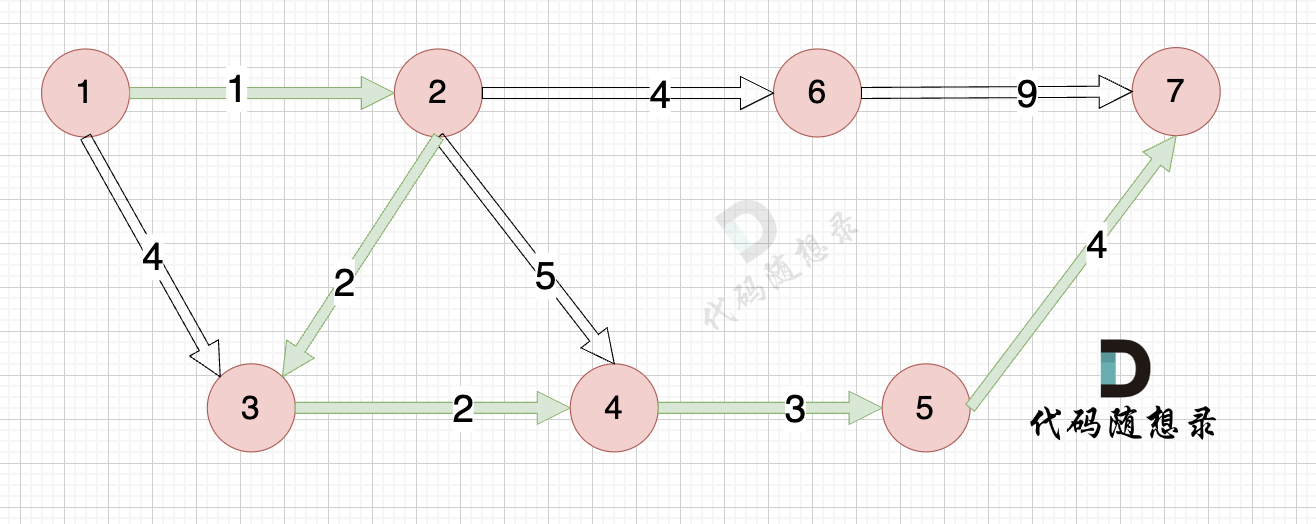
在上面的讲解中，每一步 我都是按照 dijkstra 三部曲来讲解的，理解了这三部曲，代码也就好懂的。

本题代码如下：

#include <iostream>
#include <vector>
#include <climits>
using namespace std;
int main() {int n, m, p1, p2, val;cin >> n >> m;vector<vector<int>> grid(n + 1, vector<int>(n + 1, INT_MAX));for(int i = 0; i < m; i++){cin >> p1 >> p2 >> val;grid[p1][p2] = val;}int start = 1;int end = n;// 存储从源点到每个节点的最短距离std::vector<int> minDist(n + 1, INT_MAX);// 记录顶点是否被访问过std::vector<bool> visited(n + 1, false);minDist[start] = 0;  // 起始点到自身的距离为0for (int i = 1; i <= n; i++) { // 遍历所有节点int minVal = INT_MAX;int cur = 1;// 1、选距离源点最近且未访问过的节点for (int v = 1; v <= n; ++v) {if (!visited[v] && minDist[v] < minVal) {minVal = minDist[v];cur = v;}}visited[cur] = true;  // 2、标记该节点已被访问// 3、第三步，更新非访问节点到源点的距离（即更新minDist数组）for (int v = 1; v <= n; v++) {if (!visited[v] && grid[cur][v] != INT_MAX && minDist[cur] + grid[cur][v] < minDist[v]) {minDist[v] = minDist[cur] + grid[cur][v];}}}if (minDist[end] == INT_MAX) cout << -1 << endl; // 不能到达终点else cout << minDist[end] << endl; // 到达终点最短路径}

• 时间复杂度：O(n^2)
• 空间复杂度：O(n^2)

总结

拓扑排序精讲：
拓扑排序是针对有向无环图（DAG）的一种排序算法，目的是将图中的所有顶点排成一个线性序列，使得对于任何一条有向边(U \rightarrow V)，顶点(U)都在顶点(V)的前面。这个过程可以用来检测图中是否存在环，因为如果无法完成排序，则说明图中有环。拓扑排序的关键在于每次选择入度为0的顶点加入排序结果，并更新相关顶点的入度。

Dijkstra（朴素版）精讲：
Dijkstra算法是一种计算单源最短路径的算法，适用于边权重为非负数的图。它通过维护一个距离数组，记录源点到所有其他顶点的已知最短距离，然后不断更新这个距离数组来找到最短路径。朴素版的Dijkstra算法使用简单的循环来更新距离，没有使用优先队列，因此效率较低，但其核心思想是贪心地选择当前最短的未处理顶点，并更新其相邻顶点的距离。

拓扑排序的经典例子：
假设有一个课程学习系统，其中课程间存在先修要求，比如：

• 课程A是课程B的先修课
• 课程B是课程C的先修课
  拓扑排序可以用来确定一个满足所有先修要求的课程学习顺序。例如，一个有效的学习顺序可能是A→B→C。

Dijkstra算法（朴素版）的经典例子：
考虑一个带权的有向图，表示城市间的道路和距离，例如：

• 城市A到城市B的距离是3
• 城市A到城市C的距离是9
• 城市B到城市C的距离是2
  Dijkstra算法可以用来找到从城市A出发到其他所有城市的最短路径。在这个例子中，从城市A到城市C的最短路径是A→B→C，总距离为5。