今年七月,AlphaProof 在国际数学奥林匹克(IMO)中斩获银牌,成功解答了四道难题(p1, p2, p4 和 p6),这一工作也让形式化进一步出圈。
本系列探讨 IMO 的相关工作,并结合当前最先进的 AI 模型表现,分享个人的思考见解。本篇讨论第一题,包括两部分内容:
第一部分:数学角度的题解分析
- 讲解问题思路,拆解解题过程
- 分析 AlphaProof 的解题方法
第二部分:形式化角度的代码分析
- IMO 形式化的相关资源
- 解题代码中存在的问题、缺陷与不足之处
- AlphaProof、o1 以及人类解法的共性探讨
- 关于证明的可解释性
P1 是 IMO 中难度最低的题目,大多数参赛者都能取得满分。之前分析了 OpenAI-o1 在此问题上的表现:尽管推理结果正确,但在证明过程中存在纰漏,要么在关键步骤胡说八道,要么一笔带过,蒙混过关。
- OpenAI-o1 分析实测 | IMO2024 第一题
接下来,我们将从人类视角分析解题思路与过程,并与 AlphaProof 提供的解答方法进行对比。
题解分析
首先,来看第一题的内容:

在探讨开始前,不妨尝试自行解决该问题:思考解答以及推导证明。
常规解题
答案思考:一眼数列求和,求和公式 1+2+...+n = n(n+1)/2 包含因子 n。容易想到 α \alpha α 取整数,特别地,分母 2 使得 α \alpha α 必须是偶数。
证明目标: α \alpha α 取全体偶数为题目所求。
推理和思考过程:
-
若 α \alpha α 为偶数,则问题显然成立。以下是证明步骤:
设 α = 2 k \alpha = 2k α=2k,那么
⌊ 1 α ⌋ + ⌊ 2 α ⌋ + ⋯ + ⌊ n α ⌋ = n ( n + 1 ) 2 α = n ( n + 1 ) k \lfloor 1\alpha \rfloor + \lfloor 2\alpha \rfloor + \cdots + \lfloor n\alpha \rfloor = \frac{n(n+1)}{2} \alpha = n(n+1)k ⌊1α⌋+⌊2α⌋+⋯+⌊nα⌋=2n(n+1)α=n(n+1)k
由于等式被 n n n 整除,只需证明: α \alpha α 必为偶数。 -
由于命题对任意正整数 n n n 成立,取 n = 2 n=2 n=2 推出 α \alpha α 为奇数时不成立。故只需证: α \alpha α 必为整数。
-
为了证明整数性,通常的技巧是:分离小数部分并证明其为0。
设 α = ⌊ α ⌋ + b \alpha = \lfloor \alpha \rfloor + b α=⌊α⌋+b,其中 0 ≤ b < 1 0 \leq b < 1 0≤b<1 表示小数部分,只需证明: b = 0 b = 0 b=0。 -
为利用 α \alpha α 取偶数的性质,可以设
α = 2 k ± b , 0 ≤ b < 1 \alpha = 2k \pm b,\ 0 \leq b < 1 α=2k±b, 0≤b<1
只需证明: b = 0 b = 0 b=0。
而利用对称性,不妨设 α = 2 k + b \alpha = 2k + b α=2k+b。
此时,进入证明的关键步骤:借助题干信息,构造特殊的 n n n 来迫使 b = 0 b = 0 b=0。
常见的技巧是取极值,利用极大或极小条件导出矛盾。
反设 b ≠ 0 b\neq 0 b=0,针对取整,很自然想到构造:取最小的正整数 m m m 使得 ⌊ m b ⌋ ≥ 1 \lfloor mb \rfloor \geq 1 ⌊mb⌋≥1,即
m = min { n ∈ Z ≥ 1 ∣ ⌊ n b ⌋ ≥ 1 } m = \min\{n\in \mathbb{Z}_{\geq 1}\mid \lfloor nb \rfloor \geq 1\} m=min{n∈Z≥1∣⌊nb⌋≥1}
换言之:
⌊ m b ⌋ ≥ 1 , ⌊ ( m − 1 ) b ⌋ = 0 \lfloor mb \rfloor \geq 1,\ \lfloor (m-1)b \rfloor =0 ⌊mb⌋≥1, ⌊(m−1)b⌋=0
此时,原式可化简为
⌊ 1 α ⌋ + ⌊ 2 α ⌋ + ⋯ + ⌊ m α ⌋ = ⌊ 2 k + b ⌋ + ⌊ 2 ( 2 k + b ) ⌋ + ⋯ + ⌊ 2 m k + m b ⌋ = k ( m + 1 ) m + ⌊ b ⌋ + ⌊ 2 b ⌋ + ⋯ + ⌊ m b ⌋ = k ( m + 1 ) m + ⌊ m b ⌋ ≡ ⌊ m b ⌋ m o d m \begin{align*} &\lfloor 1\alpha \rfloor + \lfloor 2\alpha \rfloor + \cdots + \lfloor m\alpha \rfloor \\ = &\lfloor 2k + b \rfloor + \lfloor 2(2k + b) \rfloor + \cdots + \lfloor 2mk + mb \rfloor \\ = &k(m+1)m + \lfloor b \rfloor + \lfloor 2b \rfloor + \cdots + \lfloor mb \rfloor\\ = &k(m+1)m + \lfloor mb \rfloor\\ \equiv & \lfloor mb \rfloor \mod m \end{align*} ===≡⌊1α⌋+⌊2α⌋+⋯+⌊mα⌋⌊2k+b⌋+⌊2(2k+b)⌋+⋯+⌊2mk+mb⌋k(m+1)m+⌊b⌋+⌊2b⌋+⋯+⌊mb⌋k(m+1)m+⌊mb⌋⌊mb⌋modm
根据题意, m m m 整除 ⌊ m b ⌋ \lfloor mb \rfloor ⌊mb⌋。同时,因为
1 ≤ ⌊ m b ⌋ ≤ ⌊ m ⋅ b ⌋ < ⌊ m ⌋ = m 1 \leq \lfloor mb \rfloor \leq \lfloor m\cdot b \rfloor < \lfloor m \rfloor = m 1≤⌊mb⌋≤⌊m⋅b⌋<⌊m⌋=m
而 m m m 不可能整除比自身小的正整数,导致矛盾。
证毕。
思考过程
我们的推理证明树大致如下:
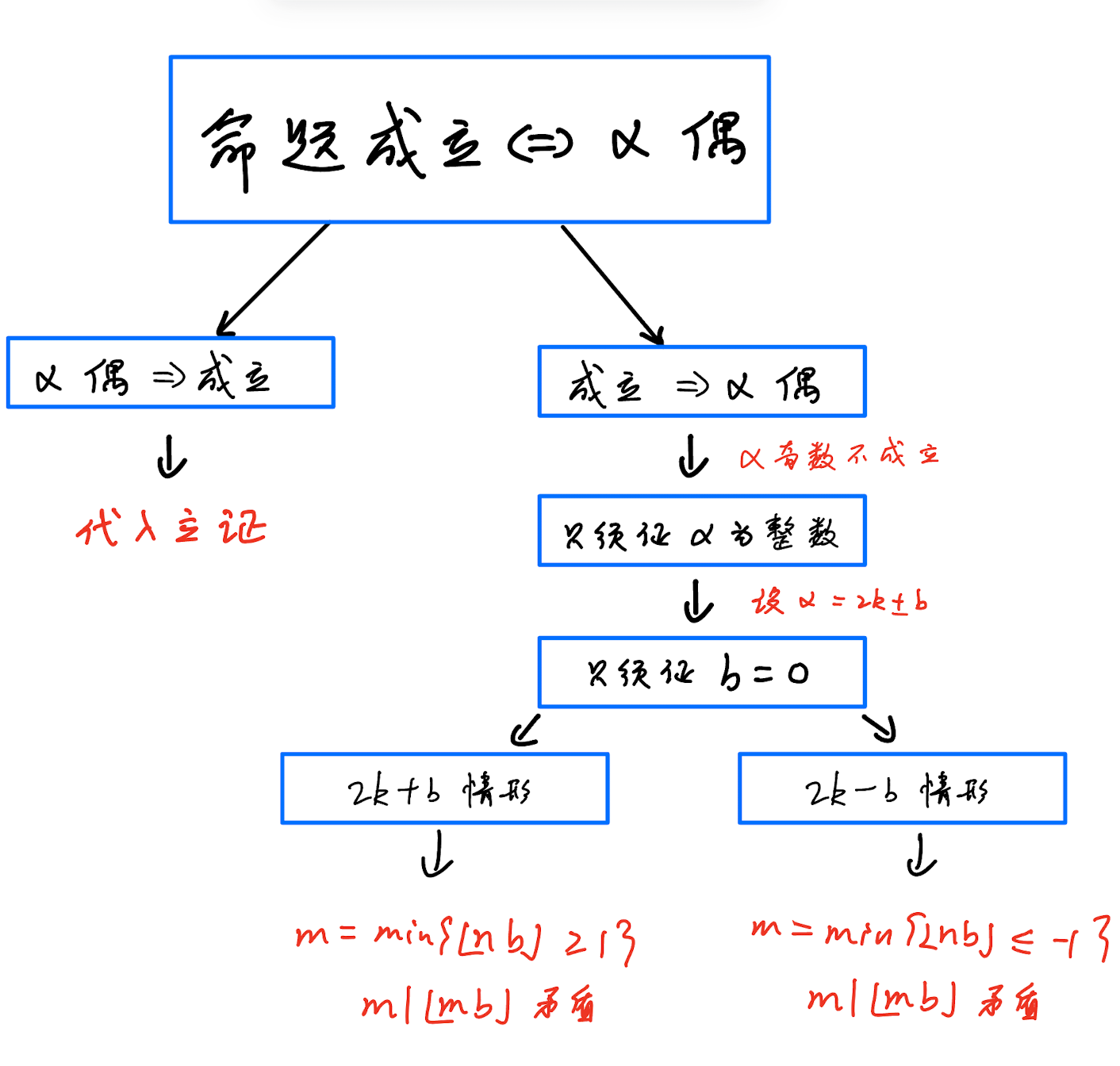
用三元组总结我们对该题的联想思考:
- (
1+2+...+n, 触发联想, 求和公式) - (证明整数, 常规策略, 令 α = ⌊ α ⌋ + b \alpha=\lfloor \alpha \rfloor + b α=⌊α⌋+b)
- (证明偶数, 常规策略, 令 α = 2 k ± b \alpha = 2k\pm b α=2k±b)
- (构造矛盾, 常规策略, 取极大极小值)
一般地,我们在日常训练中建立这些联想,建立对左侧条件的敏感性。在解题过程中,这些经验联想引导我们生成策略,转化证明目标,最终证明问题。而“生成策略”+“转化目标”的过程,与 LEAN 的 tactic 策略 + proof state 机制非常相像。
官方题解
IMO UK 官方提供了四种解法,核心思想都是通过选择“足够大的 n”来推导矛盾。
实测 DeepSeek 和 GPT-4o 也采用了基于 α = ⌊ α ⌋ + b \alpha = \lfloor \alpha \rfloor + b α=⌊α⌋+b 的构造方向,但错误地得出: α \alpha α 取所有整数。

而 OpenAI的 o1 虽然结论正确,但证明过程存在错误:缺乏竞赛经验的积累,未能应用取极值以证矛盾的技巧。
补充:IMO-UK 最近更新了一版题解,第一题新增了用有理数的构造性证明,详情参见:IMO-solutions-updated.pdf。
AlphaProof 题解
AlphaProof 与前边提到的几种解法有所不同,整体采用构造性的方法。先证明偶数成立,将问题转化为证明 α \alpha α 必为偶数。证明树大致如下,关键在右侧分支:
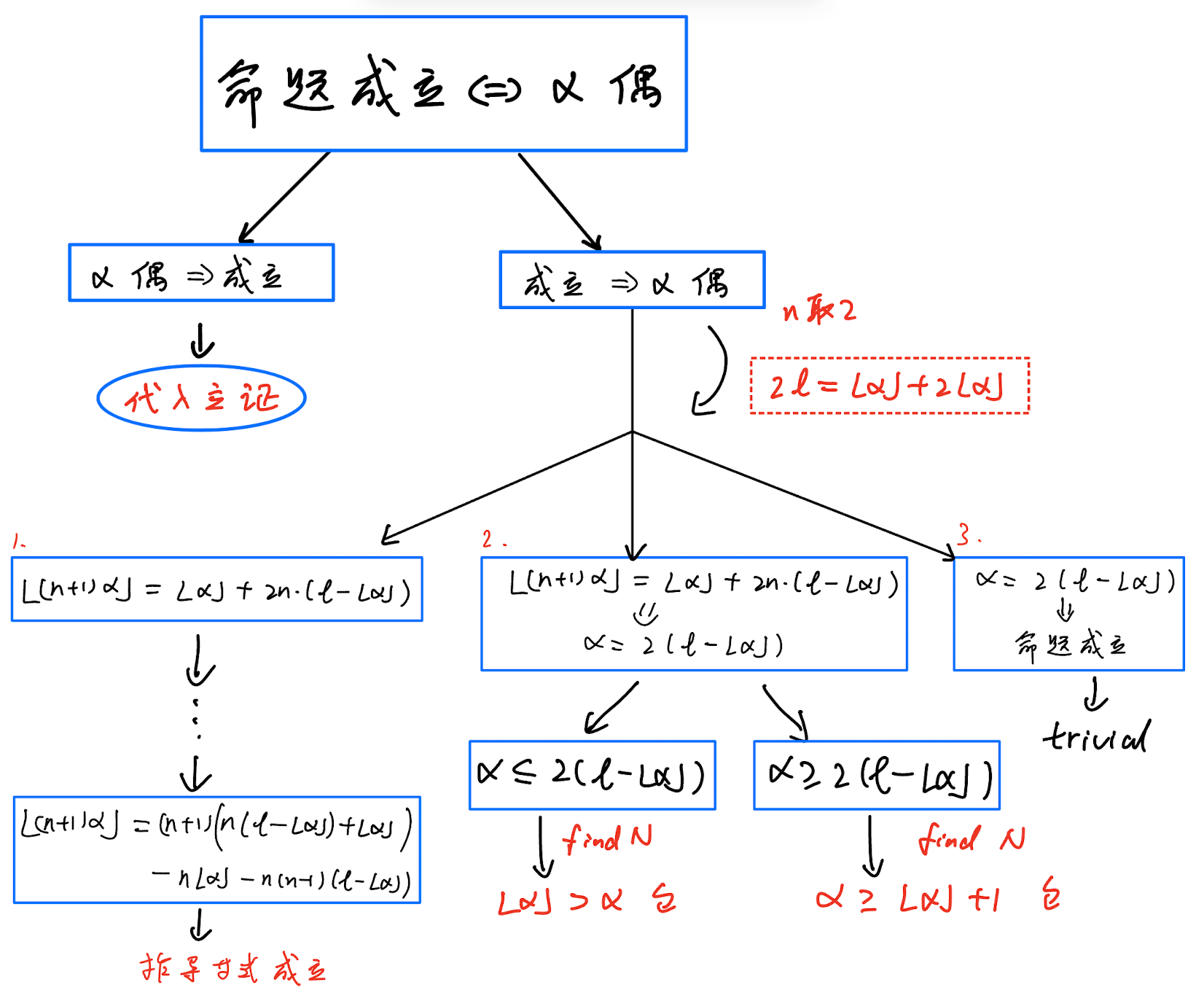
将题干条件取 n = 2 n=2 n=2 得到变量 l l l:
2 l = ⌊ α ⌋ + ⌊ 2 α ⌋ , ∃ l ∈ Z 2l = \lfloor \alpha \rfloor + \lfloor 2\alpha \rfloor,\ \exists \ l \in \mathbb{Z} 2l=⌊α⌋+⌊2α⌋, ∃ l∈Z
变形得:
⌊ α ⌋ = 2 l − ⌊ 2 α ⌋ = 2 ( l − ⌊ α ⌋ ) \lfloor \alpha \rfloor = 2l - \lfloor 2\alpha \rfloor = 2(l - \lfloor \alpha \rfloor) ⌊α⌋=2l−⌊2α⌋=2(l−⌊α⌋)
受这个式子启发,只需证明如下公式, α \alpha α 即为偶数:
α = 2 ( l − ⌊ α ⌋ ) ( 1 ) \alpha = 2(l - \lfloor \alpha \rfloor) \quad (1) α=2(l−⌊α⌋)(1)
到这一步还能理解。接下来是一系列的公式构造,有点强算的味道。将公式 (1) 的转化为公式(2):
⌊ ( n + 1 ) α ⌋ = ⌊ α ⌋ + 2 n ( l − ⌊ α ⌋ ) ( 2 ) \lfloor (n+1)\alpha \rfloor = \lfloor \alpha \rfloor + 2n(l-\lfloor\alpha \rfloor)\quad (2) ⌊(n+1)α⌋=⌊α⌋+2n(l−⌊α⌋)(2)
具体地,我们需要证明两个内容:
- 引理:公式 (2) 能推出公式(1)。
⌊ ( n + 1 ) α ⌋ = ⌊ α ⌋ + 2 n ( l − ⌊ α ⌋ ) ( 2 ) ⇒ α = 2 ( l − ⌊ α ⌋ ) \begin{align*} &\lfloor (n+1)\alpha \rfloor = \lfloor \alpha \rfloor + 2n(l-\lfloor\alpha \rfloor)\quad (2)\\ &\Rightarrow \alpha = 2(l-\lfloor \alpha \rfloor) \end{align*} ⌊(n+1)α⌋=⌊α⌋+2n(l−⌊α⌋)(2)⇒α=2(l−⌊α⌋) - 公式 (2) 成立。
⌊ ( n + 1 ) α ⌋ = ⌊ α ⌋ + 2 n ( l − ⌊ α ⌋ ) \lfloor (n+1)\alpha \rfloor = \lfloor \alpha \rfloor + 2n(l-\lfloor\alpha \rfloor) ⌊(n+1)α⌋=⌊α⌋+2n(l−⌊α⌋)
引理用了等式转为不等式的技巧,结合反证法证明:
α ≤ 2 ( l − ⌊ α ⌋ ) ∧ α ≤ 2 ( l − ⌊ α ⌋ ) \alpha \leq 2(l-\lfloor \alpha \rfloor) \land \alpha \leq 2(l-\lfloor \alpha \rfloor) α≤2(l−⌊α⌋)∧α≤2(l−⌊α⌋)
所以,压力来到了公式(2)。往下还有一系列的形变构造。整个过程带有“大力飞砖”的感觉,多次使用“为了证明…,只需证明…”的迭代,生成了冗长的过程。
形式化角度
前边从数学角度分析了 AlphaProof 的解题思路。接下来,根据其生成的 LEAN 代码分析其解题过程。
IMO 形式化
AlphaProof 采用了 F2F 的形式,即从形式化命题输入出发,产生形式化证明。在提供形式化命题时,需要将问题答案一并输入,这在某种程度上简化了问题。不过,证明才是最困难的部分。
DeepMind 在其博客中提供了:
- 题解代码
- 支持交互展示的 Demo
- 以及技术分析报告。
我们在 Lean-zh/IMO_2024 仓库也把相关的 Lean 代码和环境做了整理。
此外,Lean 社区对 AlphaProof 的讨论 非常活跃,摘取关于 IMO 代码的几个工作:
- AlphaProof 生成的题解代码表述晦涩,且存在冗余的记号。一些工作对其内容进行了整理简化。
- 用动画化的方式,展示 p1, p2, p6 证明过程中策略与状态的变化。
- compfiles 项目:用 Lean4 形式化奥赛数学题,目前涵盖了 42 道 USAMO 问题和 137 道 IMO 问题(包括今年的 P1, P2, P3 和 P6)。
- Mathlib Archive 中收录了许多 IMO 题解,包括今年的 P1, P2 和 P6 题目,证明均由人工编写,未使用 AlphaProof 生成的证明。
代码分析
形式化后的命题如下:
theorem imo_2024_p1 :{(α : ℝ) | ∀ (n : ℕ), 0 < n → (n : ℤ) ∣ (∑ i in Finset.Icc 1 n, ⌊i * α⌋)}= {α : ℝ | ∃ k : ℤ, Even k ∧ α = k} := by
自然语言解释:
- 等式左侧的集合: α \alpha α 是一个实数,并且对于任意自然数 n n n,当 n > 0 n > 0 n>0 时,整数 n n n 整除求和式 ∑ i = 1 n ⌊ i ∗ α ⌋ \sum_{i=1}^{n}\lfloor i * \alpha\rfloor ∑i=1n⌊i∗α⌋。
- 等式右侧的集合: α \alpha α 是一个实数,存在某整数 k,且 k 是偶数,同时满足 α = k \alpha = k α=k。
这是人类形式化的命题,所以很好阅读和理解。但 AlphaProof 的题解代码就很难读了,且存在怪异的表达方式和符号。
比如第 1 题略写了空格,以及难懂的 lambda 抽象:
useλy . x=>y.rec λS p=>?_
第 2 题在使用归纳法时,开头用 (10)+2 来表达 12
induction(10)+2
第 6 题的冗余表达,把 u (-a) 复杂化成 (u<|@@↑(( (-a ))));以及大量多余的括号:
have:=(this<| -a) (↑a + (((u a))): (↑_ :((( _) ) ) )) ..
简化版本:
have:=(this<| -a) (↑a + u a: (↑_ : _ ) ) ..。
根据这些观察,AlphaProof 似乎在字符级别进行采样,与传统的前提选择(premise selection)有所不同。
解题方式
目标分解策略
证明过程存在一些有趣的现象,比如 多次使用 suffices 策略:这允许我们分解目标,允许正推和逆推,契合人类的思维方式。
比如 A -> E 需要经历 A -> B -> C -> D -> E 的过程,suffices C 允许把证明序列拆解成 A -> C 和 C -> E 两段。
不过,这个方式会可能产生无用的子目标。例如,第 2 题的代码花费了 16 行生成了一个简洁却未被使用的结论 a + b | g。
The agent wastes the next 16 lines proving then discarding a lemma
关于目标分解,今年在 ICLR 上有一些相关研究:
- 分解证明步骤,以进行句子级别验证的 StepProof
- 鼓励 LLMs 提出新引理并进行证明的 ProD-RL
- 关注子目标和过程的 SubgoalXL 和 FormL4 等
我们将会在后续出一期整理和介绍。
探索与优化
尽管 AlphaProof 的代码中存在晦涩的记号、复杂化的表述和多余的步骤,只要证明的关键逻辑保留在其中,就不影响最终解题结果。
这与人类的解题过程相似:我们会尝试不同方案,产生无关的结论,但确定答案后,我们会精简过程,过滤掉冗余结论。
AlphaProof 缺少了后期优化的阶段。或许可以训练一个单独的网络来改进证明,这不像找到证明那么难。
两阶段学习
这也体现了一种“两阶段学习”的过程,正如数学家华罗庚所说:学习是由薄到厚,再由厚到薄的过程。第一阶段,思维发散(薄到厚),类似于蒙特卡洛树搜索,广泛尝试不同思路;第二阶段,归纳总结(厚到薄),在取得阶段性成功后进行整理。
o1 模型解题也是这种模式:思考阶段探索答案,思考完成后,输出凝练的解题过程。
毕竟,让模型一步到位是比较苛刻的,就好比解题时不允许使用草稿。
组合题与编程
AlphaProof 未能解决的 P3 和 P5 是组合题,组合问题通常借助编程能更好地找到答案。例如,今年的 AIMO 最佳工作 Numina 就使用了编程推理来计算答案。
而这里 P3 可以程序计算寻找规律,P5 则可借助模拟仿真获得思路。不过,组合问题本身的形式化也比较麻烦。
证明的意义
可理解性
通常,我们可以学习他人的解题思路,积累技巧。但 AlphaProof 的证明逻辑很强行。除了告诉我们答案是对的,带来的收获不多。
之前聊过,数学除了严谨证明,还应该能带来对问题的理解:
- 陶哲轩:数学不仅仅是严谨性和证明
LEAN 将数学证明变成了游戏,理想情况下,这种“通关”体验应带来反思和领悟,而不仅仅是解决问题。
正如最近大火的《黑神话·悟空》,玩家在探索过程中经历磨练和挑战,邂逅不同人物和故事,这些过程也贡献了我们对游戏的理解。
就好比,有人告诉你黎曼猜想是对的,因为有个可靠的机器验证过了。这很棒,基于黎曼猜想的结论都成为定理了。但同时,这个回答很空洞,人们知道猜想对了,但不知道为什么对,内心里的疙瘩还是不能消除。
动态的可理解性的
关于这点,社区的一段对话挺有意思。

对于机械性的步骤和想法,我们希望机器帮我快速验证。但是对于定理核心,我希望能得到一个可以理解的证明。这些可以让我们减少试错成本,更加专注到对定理核心证明的理解。
例如,在证明 A -> C 时,设想 B 是可能的中间步骤。但我们不确定 A -> B 是否成立,虽然验证并不困难,但相当琐碎。如果模型可以协助确认 A -> B 的可行性,我们便能果断跳过这一环节,并聚焦于 B -> C 的证明。
总结
以上,我们从数学和形式化两个角度对 AlphaProof 的工作进行了深入分析。
除此之外,模型技术角度也有许多值得深入研究的内容,包括数据合成方式、策略空间定义以及搜索算法等等。关于这些,我们在 AI 与 IMO 的相关工作时简单聊过:
- AI 改写数学竞赛 | 从 IMO Grand 到 AlphaProof
后续系列中再进一步整理介绍。


C 预处理器)
)


)
:神经网络与迁移学习在猫狗分类中的应用)