参考视频:标量、向量、矩阵、张量-机器学习-李文哲AI人工智能培训_哔哩哔哩_bilibili
参考资料:深度学习基础:标量、向量、矩阵、张量_深度学习本质是矩阵-CSDN博客
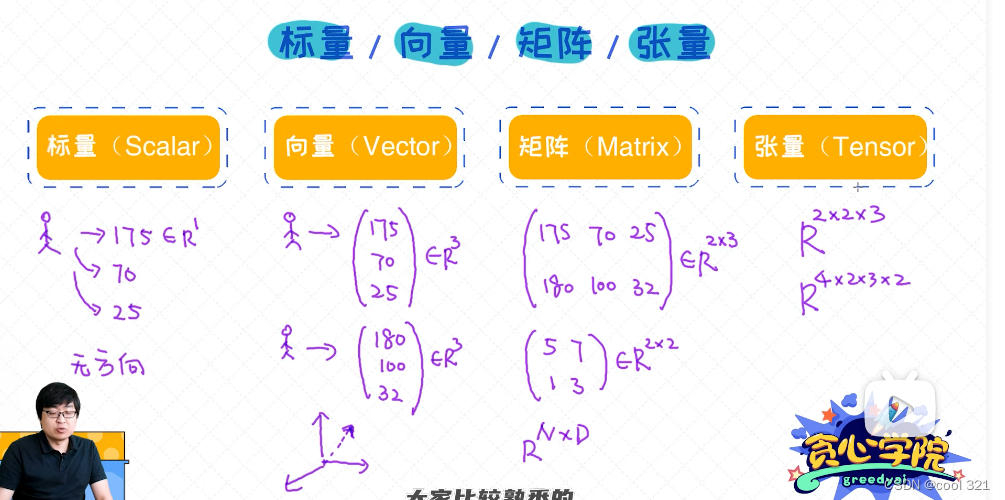
标量是一个独立存在的数,比如线性代数中的一个实数5就可以被看作一个标量,所以标量的运算相对简单,与平常做的算数运算类似。
向量指一列顺序排列的元素,我们通常习惯用括号将这些元素扩起来,其中每个元素都又一个索引值来唯一的确定其中在向量中的位置。多个标量组成向量。
矩阵是二维数组,其中的每一个元素被两个索引而非一个所确定。多个向量组成矩阵。
在几何代数中,张量是基于向量和矩阵的推广,通俗一点理解的话,我们可以将标量是为0阶张量,矢量视为一阶张量,矩阵视为二阶张量,例如一张彩色图片,可以表示成一个三阶张量,因为彩色图片的每个像素点可以看成一个(RGB)3*1的矩阵[12,242,43](也可以看作二维张量),然后我们把这些像素点拼接成一个面,就变成了三维张量。多个矩阵组成张量。
代码举列:
import torch# 创建示例张量
v = torch.randn(1, 1, 48, 25600)
k = torch.randn(1, 1, 25600, 1)# 进行矩阵乘法
y = torch.matmul(v, k)# 输出形状
print(y.shape) # 输出形状为 [1, 1, 48, 1]
根据矩阵乘法的规则,两个矩阵可以相乘的条件是前一个矩阵的最后一个维度与后一个矩阵的倒数第二个维度相等。这里 v 的最后一个维度是 25600,k 的倒数第二个维度也是 25600,所以可以进行矩阵乘法。





