#1024程序员节 | 征文#
进行逻辑结构设计之后,原本的数据借助表格(即关系)的方式变得一目了然,方便了数据的查询、插入、更新、修改。但要真正设计一款好的数据库并不止步于此,关系中的数据也不单单靠简单的二维表组织,还需要规范的设计理论来提高数据库的可靠性,提高效率,减少数据冗余。
规范化设计理论
函数依赖
初步介绍
逻辑结构设计用关系模型将数据从E-R模型变成关系,而关系模型中实现数据库规范化的一个重要理论是函数依赖,它指的是属性之间的约束关系,“约束”就像参照完整式约束中当关系A中的主键确定了,那么引用关系B的外键也就随之确定了,再比如用户定义完整式约束中当属性是age时属性值的域也就注定不能是负数,再或者是实体完整性约束中一个属性一旦是主键那么其下的属性值就不能出现空值和重复的情况,要满足唯一性和非空性。这里的函数依赖也是一样,只不过是描述属性之间的约束关系。比如属性A是国家,属性B是首都,那么一旦当属性A里的值确定了,属性B的值也就随之确定了。函数本身表示的就是输入一个值根据一个规则然后输出唯一一个特定的值,用f(x)表示,x表示输入的参数,f表示function即函数规则,那么F(x)就是输出的参数。比如学生表中作为主键的学号是输入参数,那么根据该关系中的函数依赖规则,输出参数则是对应学生的姓名和学生的系别。
Sname=f(Sno),Sdept=f(Sno)
即Sno函数决定Sname
Sno函数决定Sdept
记作Sno→Sname,Sno→Sdept函数依赖更为严谨的定义是:

属性之间可以一个决定另一个,也可以互相决定。比如学生表中假如学生不允许重名那么学号和学生姓名之间就是一一对应的关系,互相依赖了。函数依赖理论要求关系中的所有值都要满足相应的规则,而且有时候函数依赖具有数据语义特征,在某种程度上时可以反映现实世界,例如学生表的例子。
来举一些例子感受一下怎么表示函数依赖
①关系Student(Sno, Sname, Sgender, Sage, Sdept)
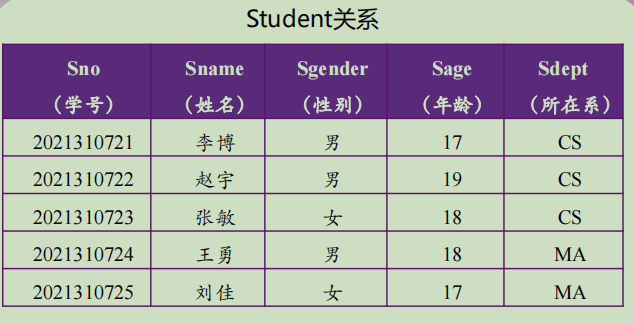
对于此关系:假设学生姓名不允许重复那么:
Sno → Sgender、 Sno → Sage、Sno → Sdept,
Sname → Sgender, Sname → Sage、Sname → Sdept②不满足函数依赖的:
![]()
③违反函数依赖的情况:
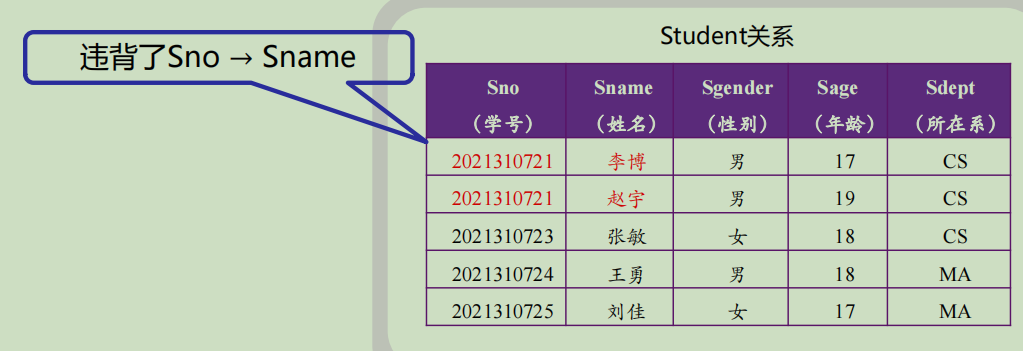
函数依赖还分为以下几种:
非平凡和平凡
X → Y,但Y⊈X,则称X → Y 是非平凡函数依赖//最常见
X → Y,但Y⊆X,则称X → Y 是平凡的函数依赖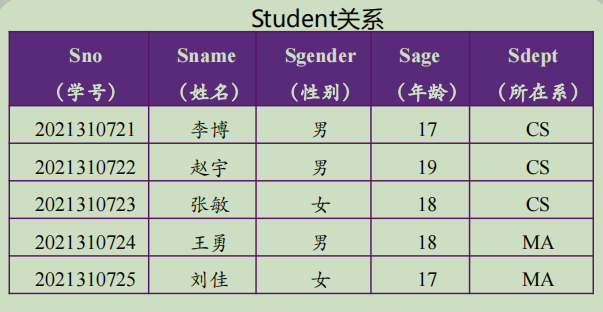
举个例子,该表中
//非平凡函数依赖
Sno → Sgender、 Sno → Sage、Sno → Sdept,
Sname → Sgender, Sname → Sage、Sname → Sdept//平凡函数依赖,所有的关系都满足平凡函数依赖,是显然易见的,甚至有些多余但是让规范设计理论的框架更加完善,视角更完整。
Sno → Sno
(Sno, Sname) → Sno
(Sno, Sname) → Sname
(Sno, Sgender) → Sgender
(Sno, Sdept) → Sdept
(Sname, Sage) → Sage完全和部分

在上面的成绩表中(Sno,Cno)→Grade,其中Grade不是X里面的一个(X是指箭头左边的属性集),且随意拎出来一个都不能得出Grade即Sno↛Grade, Cno↛Grade,这样的属于完全函数依赖,即X中的属性都对决定Y(Y是指箭头右边的属性集)起到作用。与此同时并不是所有X中的属性都起到作用的,叫部分依赖如(Sno,Cno)f→Sno,(Sno,Cno)→Cno,用更加严谨的符号表示是:
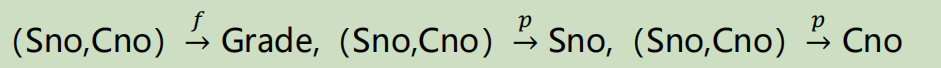
f用来表示全部(full)
p用来表示部分(partial)具体定义:

传递
如果存在X→ Y,Y ↛ X,Y → Z,那么就说Z对X有传递函数依赖,特意强调Y ↛ X是因为如果Y→X那么结合X→ Y就得出X⟷ Y,再加上Y → Z,就会变成X→Z即Z直接函数依赖于X。
例如:Cno表示课程号,Cname表示课程名,Cpno表示先修课(先修课表示在学习某门课之前必须要先学的课)
Cno → Cname, Cname ↛ Cno, Cname → Cpno
则称: Cpno 对 Cno有传递函数依赖,其中表示Cno决定Cname,但是在课程可以同名但课程号必须不同的情况下就不会出现Cname→Cno ,即课程名和课程号是一对多的情况,但是每一门课的课程名可以决定先修课是什么(比如同一门课程可能在不同的学期开设,为了区分这些不同时间开设的课程,会使用不同的课程号,但只要课程名是相同的那么先修课就是相同的)
预告一下明天写多值依赖、连接依赖和用函数依赖重新解释关系的键






——FFmpeg源码中,解析RTP header的实现)