游戏AI的创造思路-技术基础-sigmoid函数详解

在前面的机器学习和深度学习的内容中，大量出现了sigmoid函数，所以本篇为大家介绍下sigmoid函数，希望对大家理解前面的算法和后面的Transformer有所帮助

3.8. sigmoid函数

3.8.1. 定义

3.8.2. 性质

3.8.3. 应用

3.8.4. 缺点

3.8.5. sigmoid函数的导数

3.8.5.1. 导数的定义

3.8.5.2. 导数的性质

3.8.5.3. 导数的应用

3.8.5.4. 注意事项

3.8.6. Python代码实现

3.8. sigmoid函数

3.8.1. 定义

sigmoid函数是一种常见的数学函数，其形状为“S”形曲线。

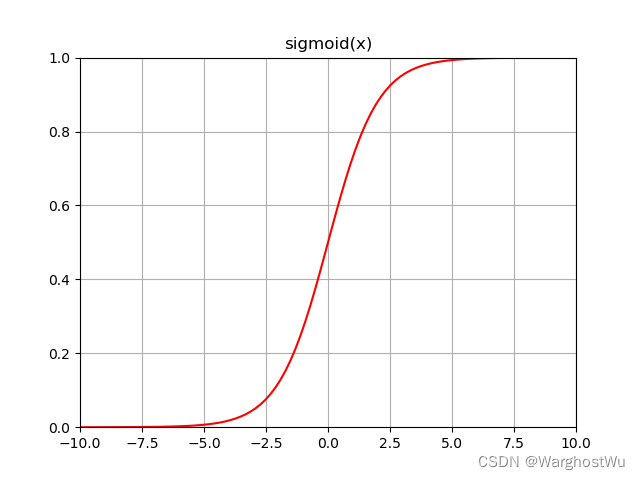
在机器学习和深度学习中，特别是在处理二分类问题时，sigmoid函数被广泛用作激活函数。

sigmoid函数的数学公式为：

$[ f(x) = \frac{1}{1 + e^{-x}} ]$

其中， $( e )$ 是自然对数的底数（约等于2.71828）。

3.8.2. 性质

值域：sigmoid函数的值域为(0, 1)，这意味着无论输入( x )是什么，输出总是在0和1之间。这个性质使得sigmoid函数非常适合用于表示概率或者将任意实数映射到(0, 1)区间内。
单调性：sigmoid函数在其定义域内是单调递增的。
可导性：sigmoid函数在其定义域内是可导的，这个性质在神经网络中非常重要，因为它允许我们使用梯度下降等优化算法来训练网络。其导数为：

$[ f'(x) = f(x)(1 - f(x)) ]$

形状：sigmoid函数的形状类似于“S”，在 $( x = 0 )$ 附近变化较快，而在远离0的地方变化较慢。这种特性使得sigmoid函数在处理一些需要非线性变换的问题时非常有用。

3.8.3. 应用

二分类问题：在机器学习中，sigmoid函数常用于二分类问题的输出层，将网络的输出转换为概率值。例如，在逻辑回归中，sigmoid函数用于将线性回归的输出转换为预测为正类的概率。
神经网络激活函数：虽然近年来ReLU（Rectified Linear Unit）等激活函数在深度学习中更为流行，但sigmoid函数仍然在某些情况下被用作神经网络的激活函数，特别是在需要输出概率或进行二分类的任务中。

3.8.4. 缺点

尽管sigmoid函数有其优点，但在深度学习中作为激活函数时也存在一些缺点：

梯度消失问题：当输入值远离0时，sigmoid函数的导数接近于0。在深层神经网络中，这可能导致梯度在反向传播过程中迅速减小，使得网络难以训练。
计算成本：sigmoid函数涉及指数运算，这在计算上可能相对昂贵，尤其是在大规模数据集和深层网络上。
非零中心化：sigmoid函数的输出总是大于0，这意味着在神经网络中，后续层的输入总是正的。这可能导致权重更新的不稳定性。

3.8.5. sigmoid函数的导数

sigmoid函数的导数表示了该函数的斜率，即函数值随输入变量变化的速率。以下是关于sigmoid函数导数的详细解释：

3.8.5.1. 导数的定义

sigmoid函数的导数定义为函数值与其补的乘积，具体公式为：

$[ f'(x) = f(x)(1 - f(x)) ]$

其中， $( f(x) )$ 是sigmoid函数的值。

这个公式表明，sigmoid函数的导数可以通过原函数的值来计算。

3.8.5.2. 导数的性质

范围：sigmoid函数的导数值在0到0.25之间。当输入值 $( x )$ 趋近于正无穷或负无穷时，导数值趋近于0；而当输入值接近0时，导数值接近其最大值0.25。
与函数值的关系：导数值与原函数值密切相关。
- 当sigmoid函数的值 $( f(x) )$ 接近1或0时，其导数值会变小，表明函数在这些区域的变化率较小。
- 相反，当 $( f(x) )$ 接近0.5（即 $( x )$ 接近0）时，导数值较大，说明函数在这一区域变化较快。

3.8.5.3. 导数的应用

神经网络训练：在神经网络中，sigmoid函数的导数对于使用反向传播算法进行权重更新至关重要。通过计算导数，我们可以了解函数值随输入变化的敏感度，并据此调整网络参数。
优化算法：在优化算法中，如梯度下降法，sigmoid函数的导数用于计算损失函数关于模型参数的梯度，从而指导参数更新的方向和步长。

3.8.5.4. 注意事项

虽然sigmoid函数的导数在神经网络训练中有其应用，但由于存在梯度消失的问题（即在函数值接近1或0时导数值很小），在深层网络中可能导致训练困难。

因此，在实际应用中需要权衡sigmoid函数的优缺点。

3.8.6. Python代码实现

import numpy as np  def sigmoid(x):  """  计算sigmoid函数值。  参数:  x -- 输入值，可以是标量、向量或矩阵  返回:  s -- sigmoid函数的值，与输入x的形状相同  """  s = 1 / (1 + np.exp(-x))  return s  def sigmoid_derivative(x):  """  计算sigmoid函数的导数。  参数:  x -- 输入值，可以是标量、向量或矩阵  返回:  ds -- sigmoid函数的导数，与输入x的形状相同  """  s = sigmoid(x)  ds = s * (1 - s)  return ds  # 示例用法  
x = np.array([1, 2, 3])  
print("Sigmoid Function Values:")  
print(sigmoid(x))  print("Sigmoid Derivative Values:")  
print(sigmoid_derivative(x))

这段代码首先定义了两个函数：sigmoid和sigmoid_derivative。sigmoid函数计算给定输入x的sigmoid值，而sigmoid_derivative函数则计算sigmoid函数在给定输入x处的导数。

在示例用法部分，我们创建了一个NumPy数组x，其中包含三个元素，并分别调用了sigmoid和sigmoid_derivative函数来计算这些值的sigmoid函数值和导数。