蒙特卡洛树MCTS和LLM相遇了会发生什么？

蒙特卡洛树MCTS和LLM相遇了会发生什么？

作者：爱工作的小小酥

原文地址：https://zhuanlan.zhihu.com/p/15852526394

导读

蒙特卡洛树是什么？

这个其实类似于之前学过的很多数据结构算法，例如深度优先搜索、广度优先搜索、并查集等等。所以，在理解这个算法的时候，可以先树立一个认知——它就是一个树结构算法。只是名字乍听起来有点高深莫测。

蒙特卡洛树如何运用到LLM中？

从OpenAI的o1模型中了解到了MCTS，后续也发现很多模型借助这种方法增强模型的推理能力。在现有结合MCTS的LLM中，大多数都是将其应用在两方面：

• 优化训练数据：使用MCTS进行数据增强，然后将新数据用于模型迭代。

• 提高复杂问题推理能力：使用MCTS扩充模型的搜索空间，使其得到更加多样的答案，然后使用相关的算法选择置信度最高的作为最终结果。

MCTS运用到LLM中时有什么不同吗？

将MCTS应用到LLM中时，会针对语言模型特点作出相应的调整，但整体思想不变，依旧按照选择、扩展、模拟、反馈四个步骤进行。在现有的方法中，改进的地方比较集中，主要是以下几点：

1、更复杂、更准确的打分模型

MCTS中非常重要的一个环节：选择节点。需要设计打分策略，计算节点的奖励值，从而减少冗余探索，以及最终选择最有价值的路径。在现有的LLM中，主要有一下设计奖励模型的方法：

• 基于规则的打分：不需要训练单独的模型，只需要和答案匹配，是否正确。

• 基于值函数的奖励模型：需要训练，和强化学习中的奖励模型类似，直接在原有的LLM后面多加一个打分的head。

• 过程奖励模型：对解题的每一个步骤打分，需要对每一步解题路径标注分数。

• 结果奖励模型：只用最终结果打分，不对步骤打分，也不需要对步骤标注奖励分数。

• 针对任务设计特殊的奖励模型：以上模型的叠加，或者设计更加复杂的计算方法，例如下面的偏好奖励模型。

2、各种各样的节点定义方法

语言模型是通过逐步解码token，生成完整的回复。其每一步的解空间相当于整个词表。因此，最直观的节点定义方法便是一个token，但为了兼容搜索速度和质量，各种启发式节点构造方法应运而生。

• 基于token的方法。将token作为一个节点。导致树太大，搜索空间太大，速度较慢。

• 基于句子的方法。将句子作为节点，搜索空间变得更大，但是树相对小一些。

• 基于解题步骤的方法。目前很多方法将COT中的每一个完整步骤作为一个节点，极大的减小了搜索空间。

• 基于完整步骤的方法。有很多self-improving方法，将完整的回复作为节点，通过让模型不断修改回复，生成下一个节点。

• 启发式定义节点候选集合。为了减少模型冗余搜索，也有很多研究者根据人类解决复杂问题的思路，定义出有限的（例如5、6个）节点集合，并针对每一种设计相应的prompt，让模型生成相应的内容。

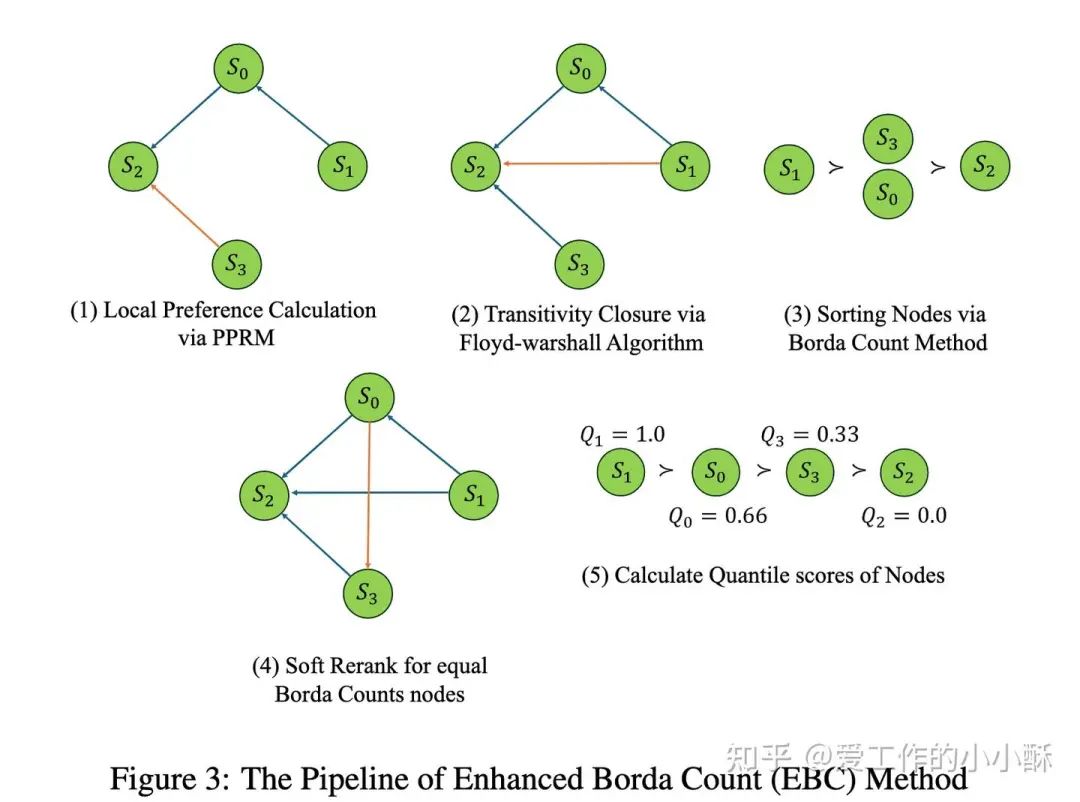
rStar—— 探索加一致性验证

论文：Mutual Reasoning Makes Smaller LLMs Stronger Problem-Solvers

论文地址：https://arxiv.org/abs/2408.06195

模型的复杂推理

不做训练能否提高模型的复杂推理效果？

目前，很多研究者认为模型是具有一定的推理能力的，只是没有发挥出来。并且，通过扩大模型的推理空间，也发现可以提高其在复杂推理任务上的性能。但这里的关键是如何扩大推理空间，以及如何在更大空间上选择正确答案？

首先讨论一下如何扩大推理空间的问题？

模型是否可以自己寻找更多可能性，答案，当然是可以！但是，在一个浩瀚的空间中寻找，势必要面临错误率较高和陷入局部最优解的困境。因此，如果让模型按照人类解决复杂问题的常规思路进行探索，是不是一个更优的方法？

其次，如何选择正确答案？

一个直观的想法，当然还是直接让原始模型自己选择，实验发现对于一个推理能力并没有那么好的模型，通过自己打分的方法和随机选择的效果差不多。

特别是在模型较小的情况下，对于原始模型来说，上述两个问题可能会更严重。在这篇论文中，通过以下两种方法实现了更好的探索和选择。

• 基于先验的MCTS

• 同行评审般的一致性选择

基于先验的MCTS

为了减轻模型的负担，减少模型的冗余探索。这篇论文根据人类常规解决复杂问题的思路，提炼出5项策略。分别是：

• A1: 生成问题的一步思考过程。

• A2: 生成剩下的所有思考过程。

• A3: 生成下一个子问题及其答案。

• A4: 重新生成子问题的答案，这一步相对于A3会多加一个COT。

• A5: 重新表述问题或子问题。

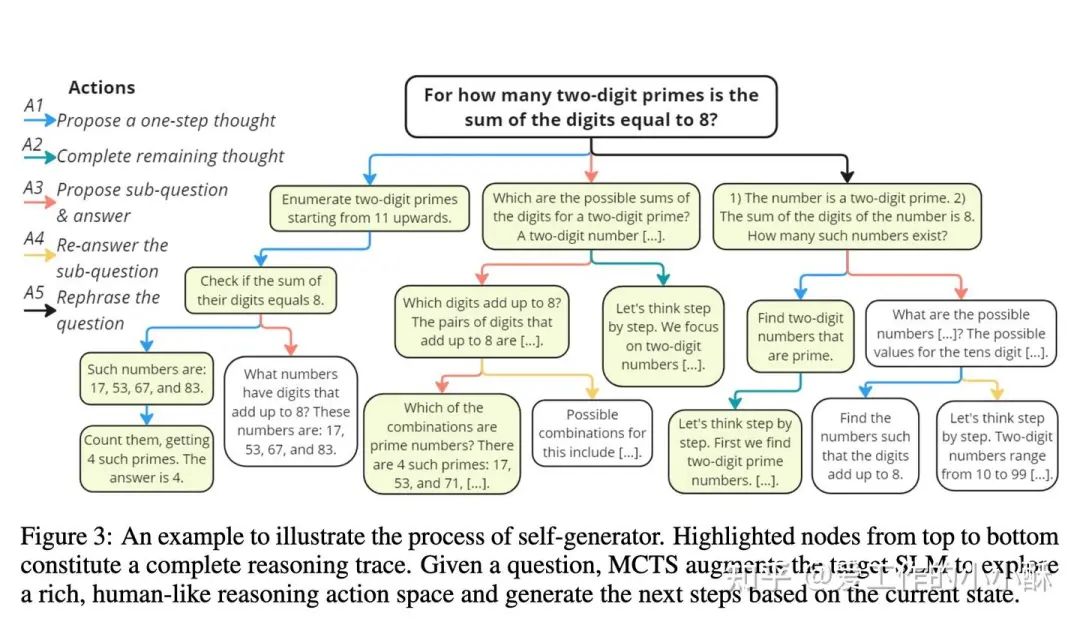
上述5个策略也可以称为原子action，在模型扩展MCTS树时，是先从action中选择一个，然后构造出相应的prompt，让模型生成相应的回答，以作为MTCS中的一个节点。并且需注意的是，A4只发生在A3的后面，A5只发生在root的后面。

有了原子行为，这篇论文直接使用了常规的构建蒙特卡洛树的方法得到了整颗树。即在每一步，使用UCT选择节点，使用上述原子action 扩展节点，模拟的时候直至到答案节点或者达到最大深度位置，然后计算节点的奖励值，反向传播给root节点。

需要注意的是，在计算奖励的时候，这篇论文采用了一致性投票，让模型生成多次答案（论文中默认是32），然后按照答案生成的频率，作为奖励值。当然，这里最终选择的答案值就是频率最高的答案。

当构建完整颗蒙特卡洛树，从多条树的路径上，可以得到多个候选答案。

同行评审般的一致性选择

对于每个题目，我们需要选择一个答案作为最终的答案，而前面也提到了，模型自己选择的能力较差（和随机选择差不多）。在这篇论文中，作者提到了一个类似「同行评审的策略」，当其他的人也认为这个人的答案是正确的时候，这个人的答案正确率一般会更高一些。

在这里，作者直接使用另一个小模型（论文中用的是Phi3-mini-4k），从候选的随机一处继续生成，如果最终得到的答案和原始模型的答案一样，就认为这个答案是对的。

按照这种方式，将通过MCTS得到多个候选答案进行过滤，剩余的候选答案，选择出奖励值最大的答案作为最终的答案。

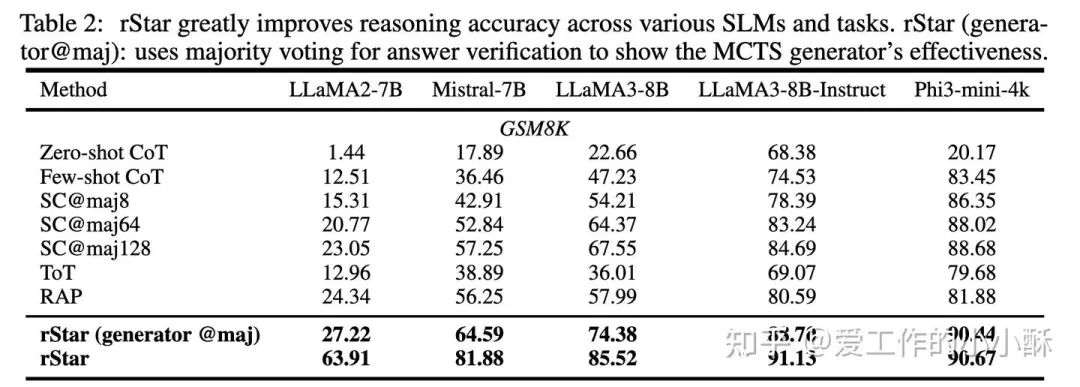
其评估结果如下：

LLaMA-Berry

LLaMA-Berry: Pairwise Optimization for O1-like Olympiad-Level Mathematical Reasoning

地址：https://arxiv.org/abs/2410.02884

如何提高模型的解题能力？COT or Self-Refine？

在复杂问题上，模型难以直接给出正确答案，一个直观的想法便是让模型一步步的给出解题步骤，最后给出答案。这个也就是经常使用的step by step的COT。其次，我们还可以让模型逐渐修正、反思自己的答案，从而给出更加合理的答案（有点类似于考试完检查）。这个过程也可以称作Self-Refine 或Reflexion。

如果上述过程是逐步进行，是否会陷入局部最优？

此时，扩大搜索空间是一个较常用的方法，并且目前大多数方法都借助MCTS实现这个目的。但当我们使用MCTS，将不得不面临如何选择最优路径问题。

选择最优路径就需要一个可以评估路径优劣的分数，在现有的方法中，经常采用数值型的PRM、ORM。但对于数学题而言，有可能存在多种解题方法都正确的情况，但总会存在一个方法更优。而基于数值的模型很难表达这种「偏好性」。

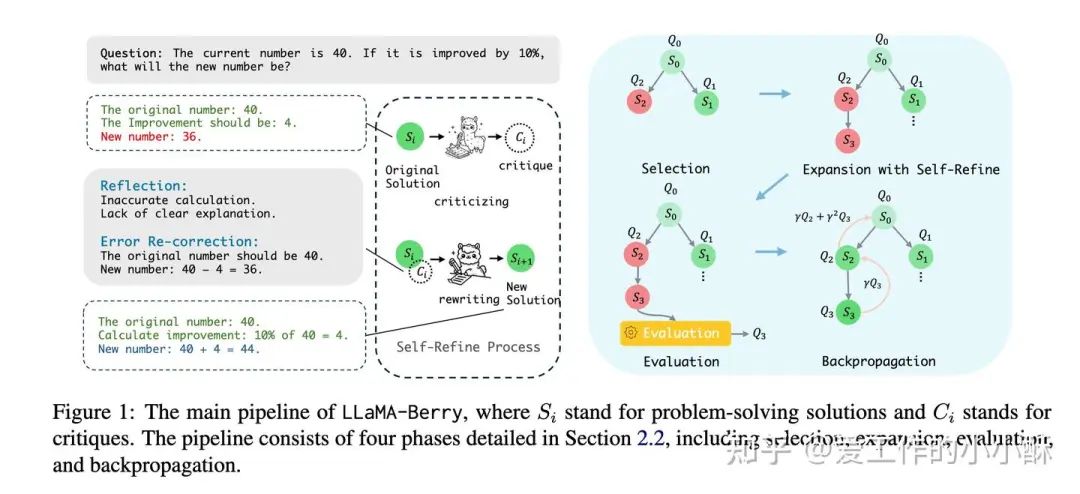
面对上述问题，这篇论文以完整步骤作为节点构建蒙特卡洛树，以Self-Refine 形式扩展其他节点。并使用DPO算法训练偏好的奖励模型（论文称作Pairwise Preference Reward Model，PPRM），可以计算全局和局部奖励分数。

构建蒙特卡洛树

和常规构建方法相比，主要在节点类型、扩展策略、奖励函数上不同。

在节点类型上，采用整个解题过程为一个节点。

在扩展策略上，使用反思+修正的方法进行，先让模型基于已有的解题过程给出存在的问题（数学符号或者逻辑错误问题），然后让模型基于已有的解题过程、反思内容重新生成新的解题过程，论文中限定最大孩子个数为2。

在奖励函数上，训练偏好模型PPRM，并同时考虑全局和局部奖励分数，下一节会详细介绍。

训练奖励模型

为了能很好的利用模型的指令遵循能力，作者将偏好数据构造成了问答的形式，例如：For Question Q, is solution a1 better than solution a2 ？ 模型回答 Yes 或 No。

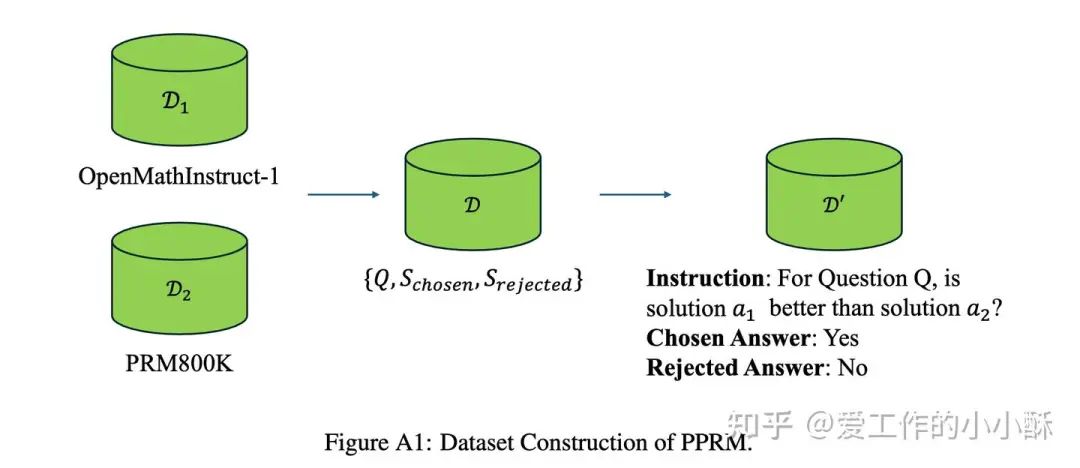
在这篇论文中，作者选用的 PRM800K 和 OpenMathInstruct-1数据集，将其改造为问答对的形式。最后使用常规的DPO在Gemma2-2B-Instruct上进行训练。

计算奖励分数

偏好模型计算的奖励分数只能代表局部奖励（两个解题路径之间的优劣），无法直接表达出在所有解题路径中的总的优势顺序。

那如何将偏好模型的得分转化为全局的优势顺序呢？

首先，对于一对解题路径来说，直接使用模型预测的logits（这里可以看做「YES」和「NO」对应的softmax值）求出其在两条路径上的概率。这里的 a1 和 a2 代表两个不同的解题路径。

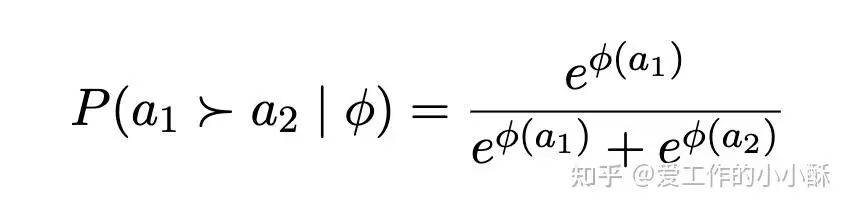
那么，将所有的解题路径合并，我们可以得到一个有向图，如果路径 ai 比路径 aj 更好的概率大于0.5，则在从 ai 向 aj 连接一条边。

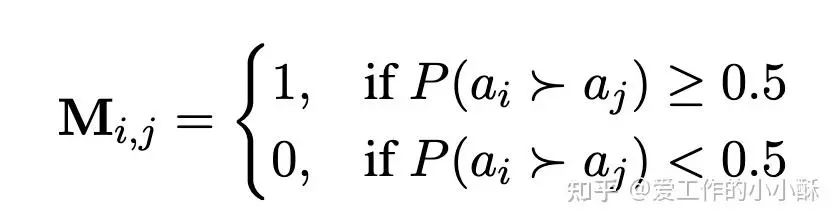
但通过这种方式得到的图有可能存在环，为了便于后续计算全局优势顺序，作者在这里使用了「传递闭包」的方法，即如果 ai 比 ak 更好， ak 比 aj 更好，则 ai 也比 aj 更好。从而得到了新的邻接矩阵C。

局部奖励分数

局部奖励计算的是当前节点在其所有孩子节点中的胜率，具体为：先从蒙特卡洛树中得到当前节点的所有孩子节点，然后根据上述计算的矩阵C计算出相对所有孩子节点的偏好优势得分总和，然后除以孩子总数，得到当前节点的局部奖励分数。

需要注意，一个节点的孩子节点不是C中相连的边，图C只是用于计算两个孩子的偏好胜负关系，不一定是蒙特卡洛树中的孩子节点。

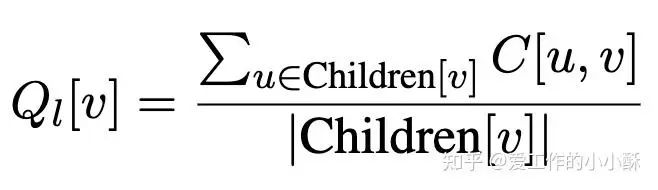
全局奖励分数

经过传递闭包得到矩阵C后，作者通过结合节点出度和原始的偏好概率得到总体排序。具体来说，首先将所有节点按照每个路径节点的出度进行排序，如果两个节点的出度一样，然后按照之前计算的概率 进行排序。

之后，使用节点的总体顺序计算全局奖励分数。

最终的奖励分数为两者的带权相加。

效果对比

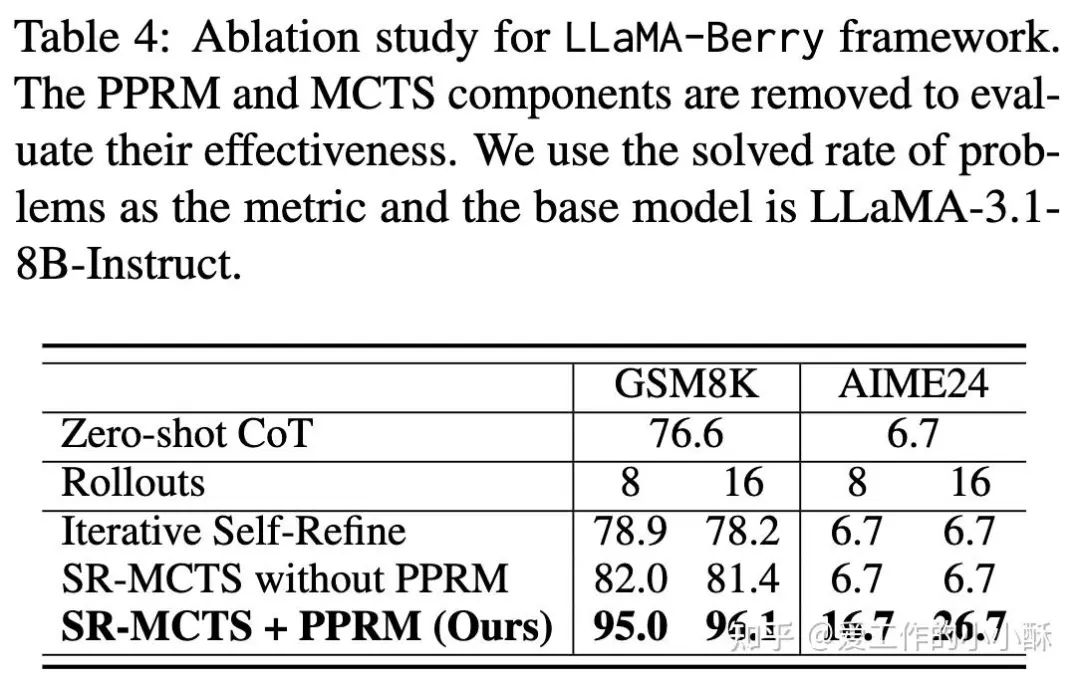
奖励模型的消融实验

作者对这篇论文中的扩展节点方法——self-refine 和 奖励模型进行了消融实验，可以发现，奖励模型在两个数据集上带来的收益都较大，但对于较难的数据集来说（AIME24)，MCTS并没有带来显著收益。

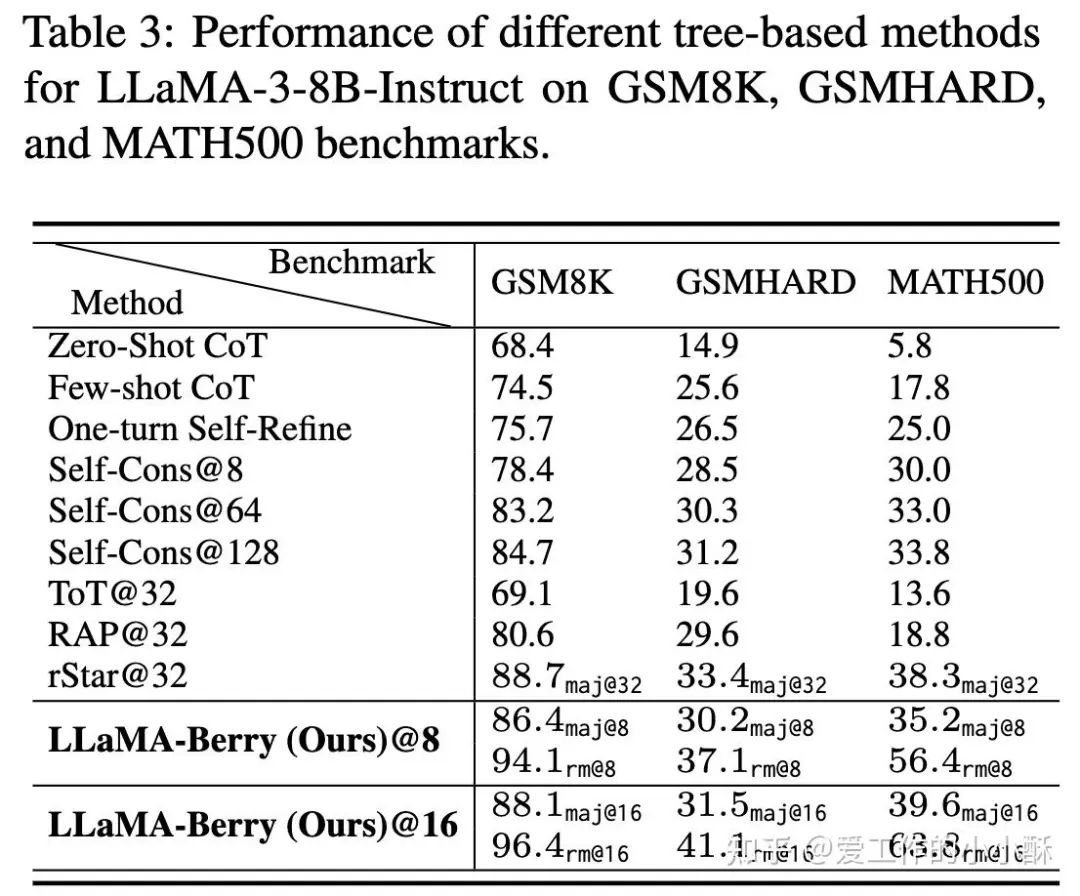
和其他树模型的效果对比

作者同样和其他采用MCTS的方法进行了对比，这里的k 代表模拟的时候进行多少次（常规情况下，MCTS的模拟会进行多次，然后使用投票方法选择最置信的答案）。

特别注意的是，这篇论文进行了两种评测：

• maj@k ：使用投票方法选择票数最高的答案，很多论文都使用这个方法，也叫做一致性选择。

• rm@k：使用奖励模型的分数选择奖励值最高的答案。

借助MCTS构造 In-Context Learning 的example

Beyond Examples: High-level Automated Reasoning Paradigm in In-Context Learning via MCTS

地址：https://arxiv.org/abs/2411.18478

在论文 rStar ，LLaMA-Berry 之后，和这两篇做了对比

整个过程没有训练，修改了现有的In-Context Learning方法，将输入的example修改为更加格式化的逻辑思考范式。

In-Context Learning是什么？

首先，让我们回顾一下什么是In-Context Learning？

In-Context Learning 顾名思义，即是在prompt中添加几个和问题相关的样例，让模型根据样例解决给出的问题。

一般情况下，会选择经典或者和问题最相关的数据作为example。但通俗来讲，直接一个可以引发模型思考的句子也可以作为example。具体可以分为以下两种方法：

（1）简短的prompt。

例如：「Let's think step by step」。这种非常考验模型本身的能力，对于复杂的问题，小模型经常还是无法解决。

（2）提供多个具体的样例。

这种就是常用的In-Context Learning方法，一般会选择几条数据添加到prompt中。但这种方法具有很多问题：

• 对输入样例的高敏感，包括样例的顺序，label的个数、样例质量。

• 缺乏最优性的样例，会影响模型生成更好的思维过程

• 难以选择最佳样例。

那么，针对上述问题，能否构造出更优的example呢？

本篇论文从人类解决的问题的角度出发，将解决问题的过程抽象化，然后将不同问题的抽象解决过程聚合，得到不同种类的抽象化步骤集合。最终，针对每个问题，选择最佳的抽象步骤作为example，以启发模型如何解决问题。

需要注意的是，这里构造的example和上面的两个常规用法都不一样了。下面详细讲解如何构造这个「抽象步骤」，论文中称作「Thought Cards」。

如何构造思维卡片？

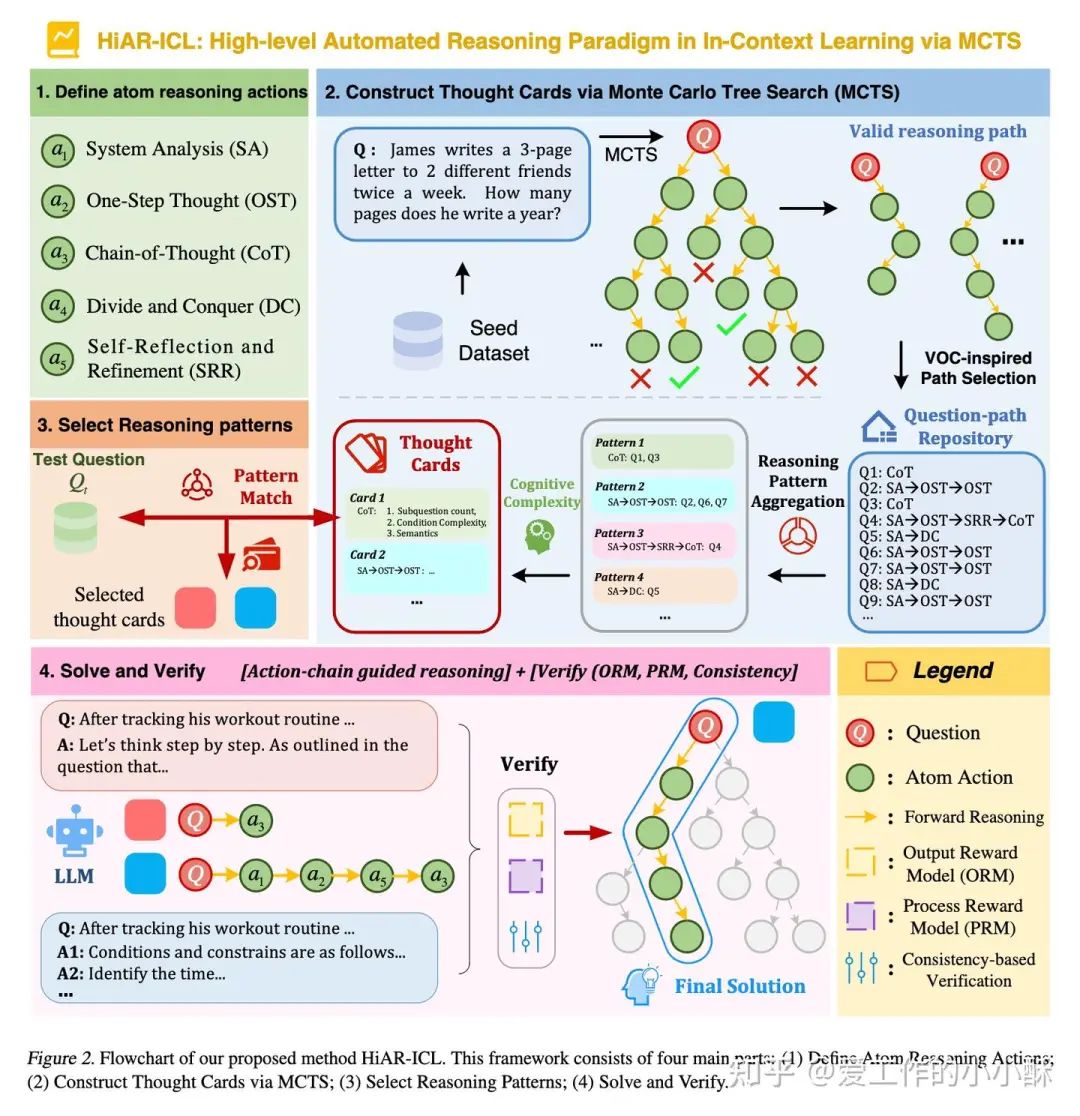
思维卡片代表了一种抽象的思维过程，在这篇论文中，会存在很多个思维卡片，在遇到一个新问题时，需要选择最佳的2-3个思维卡片，作为example提供给模型。

那这里出现了两个问题，如何选择思维卡片？如何构造思维卡片？

思维卡片包含的是一个「思维过程」，既然是过程的概念，即含有一个个的「节点」，可以实现从一步到另一步。因此，首先，我们应该创建一个个的原子节点。然后，要将这些原子节点链接为不同的思维过程。

1、创建原子节点

在这篇论文中，总共创建了5种此种节点，包括：

• System Analysis (SA)：分析问题需要的条件和限制。

• One-Step Thought (OST)：给出一步思考过程和接下来的推理步骤。

• Chain-of-Thought (CoT):给出每一步的过程，后一步需要结合上一步的结果。

• Divide and Conquer (DC):拆解子问题，并对子问题进行解决。

• Self-Reflection and Refinement (SRR):结合给出的结果，重新思考问题，并修正结果。

2、构造思维链

每个原子节点都是一个解题思路，现在关键问题是如何将多种解题思路结合在一起，进而解决一个复杂的问题？

这篇论文借助的方法便是MCTS。

通过将每一种解题思路作为树上的一个节点，经过MCTS的整个过程，构造出完整的蒙特卡洛树，然后使用相关评估算法选择最佳的路径，作为题目最终的「抽象解题步骤」。

要完成上述过程，需要先得到有标注的数据集（这样才能知道评估路径，选择正确路径），论文作者采用了一小批数据集，可以称为种子数据集。

构造MCTS

接下来的过程，便是MCTS的常规操作：从一个root节点开始，经过搜索、扩展、模拟、反向传播，构造出整棵树，然后使用奖励函数，计算各个可行路径的得分，得到最高分数路径的解题步骤。

下面着重介绍一下作者特殊处理的地方。

（1）选择。

这一步和常规一样，同样采用UCB（Upper Confidence Bounds）分数选择分数最高的节点。

（2）扩展。

这一步也和常规一样，采样上述的原子节点构造prompt，让LLM生成相应的回答。

（3）模拟

这一步就是迭代的进行选择和扩展，直至达到最大深度（论文是5）或者达到结果节点。

但稍作了一些处理，在采样原子节点的时候，为了减少冗余，让模型生成回复的时候，使用了多次一致性采样，选择最具有一致性的原子节点，进行，整个过程作者在这里进行了特殊处理，每次都重复生成多次，使用投票选择最优置信的回复，以便减少冗余分支。

（4）反向传播

这一步也和常规一样，达到结果节点后，往上依次更新「访问次数」和「价值」，价值累加过程如下：

构造数据-抽象步骤pair

通过上述过程，可以得到每条数据对应的多条解题路径，以及对应的「抽象步骤」。为了保证数据质量，作者构造了一个路径分数计算方法，选择出最优的路径作为这条数据的最佳「抽象步骤」。

这个分数综合了结果节点的价值和路径的长度，下面的 pa 代表一条路径， reward(pa|x) 即是上面的Q， C(pa) 代表了路径的长度， k 是一个超参数。

得到思维卡片

按照上述过程，每一条数据都对应了一个「抽象步骤」，然后按照「抽象步骤」的类别将上述数据聚类，然后将每一个类别下的数据抽取出3个维度上信息，以用于测试集推理。

• Subquestion Count (SC): 得到子问题数量。

• Problem Condition Complexity (PCC): 已知条件的数量。

• Semantic Similarity (SS): 评估问题和种子数据集的语义相似度。

如何选择思维卡片？

当面对一个新的数据时，首先按照上述3个维度选择topk的思维卡片，按照思维卡片的抽象步骤，推理得到多个候选结果。接下来，需要选择一个最佳的结果，论文中使用了3种常见的策略：

• process-supervision：采用Process Reward Model (PRM) 模型计算分数，论文使用的是math-shepherd-mistral-7b-prm。

• outcome-supervision：采用Output Reward Model (ORM)模型计算分数，论文使用的是Llama3.1-8B-ORM-Mistral-Data。

• 基于consistency的方法：采用Self-Consistency (SC)模型计算分数。

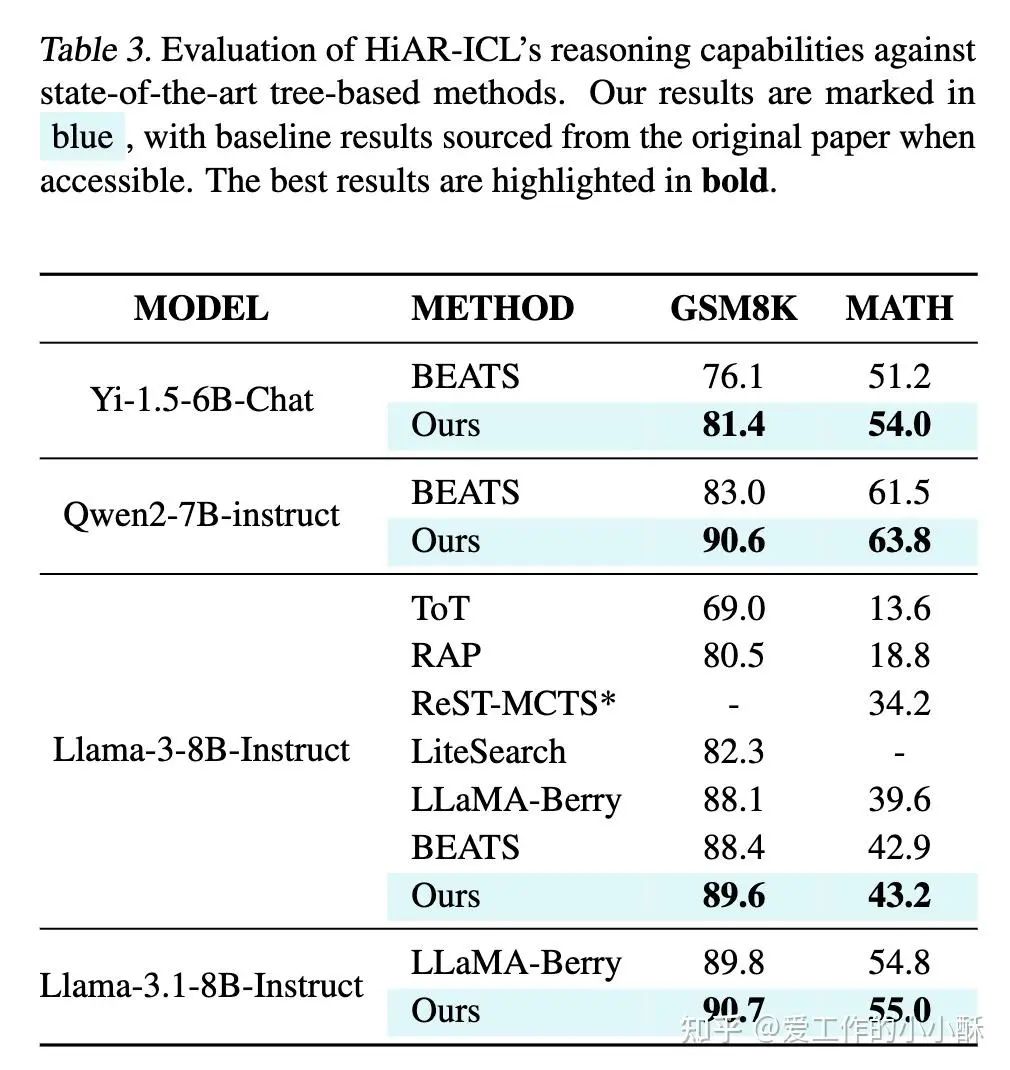
最终，此方法和现有的基于树的方法的对比如下：

ALPHALLM

Toward Self-Improvement of LLMs via Imagination, Searching, and Criticizing

地址：https://arxiv.org/abs/2404.12253

AlphaGo 强大的推理能力主要依靠的什么？

（1）大量的专家和self-play数据。大量的专家数据让其可以学习类人的策略，self-play数据可以让其使用强化学习超越人类的能力。

（2）树搜索算法扩展搜索空间。较大的搜索空间让其决策更加准确，以及会探索出更多样的策略。

（3）准确且没有歧义的反馈。象棋领域准确的胜负，可以使其得到非常准确的反馈，进行使用这个反馈更新策略。

LLM可以借鉴这种训练方法吗？

在LLM上，会存在很多难点。

（1）缺乏高质量的标注数据。专家数据标注困难，以及如何生成类似的self-play数据还未知。

（2）广阔的搜索空间。由于词表或者句子的组合情况非常巨大，导致搜索效率较低。

（3）模糊的反馈。语言模型有可能存在多个token都合适，或者多种语言表达都合理的情况，没有绝对的正确和错误，导致反馈信息模糊。

那么，会有一个折中的方案使用AlphaGo类似的方法提升模型的推理能力吗？

这篇论文就从这个角度出发，从上述3个维度设计相应的解决策略，从而优化了现有的模型训练过程。具体来说，其使用MCTS优化每一个epoch的训练数据，使得在数据量增大、数据多样性增强、数据准确性更高的情况下，按照常规的语言模型训练方法优化了模型的推理能力。整个过程也可称之为Self-improving。

数据增强

为了构造出数据量更多、多样性更强的训练数据，论文采用了「METAMATH: BOOTSTRAP YOUR OWN MATHEMATICALQUESTIONS FOR LARGE LANGUAGE MODELS」中的数据增强方法，具体来说是用现有的数据通过「改写」扩充为更多的数据，主要有以下3类：

• 答案增强：通过在prompt中增加多个样例（few-shot），开启温度采样，让模型生成不同的解题路径。然后过滤出最后答案正确的数据。

• LLM改写问题：通过设计相应的prompt，开启温度采样的情况下，让LLM对现有的问题进行多次改写。然后同样使用few-shot的方法让LLM对新问题生成解题步骤和答案，然后过滤答案正确的问题。

• 反向问题：

  • Self-Verification (SV)：随机选择原始问题的一个数值作为新的求解答案，将原始答案的信息融合到原始问题中形成新的问题描述。

  • FOBAR：和上面方法类似，只是形成新问题时，直接将答案信息作为补充信息拼接到原始问题后面。（这个较简单一些。）

例如原始问题如下：

其对应的两种反向问题方法如下：

每一个epoch都会使用上述方法对上一轮的数据进行增强。

构建蒙特卡洛树

蒙特卡洛树的节点是什么？

在语言模型中，节点的定义更多是启发式的方法，可以有很多种选择，在这篇论文中，作者采用「解题步骤」作为一个几点，论文中称作「option」。

如何扩展节点？

由于是直接设计相应的prompt，让模型基于现有的步骤生成下一个步骤，这里就会有2个问题：模型生成的重复性会不会很高？模型生成的个数需不需要限制，更多的个数对应更多的节点将会极大的影响整个搜索效率。

因此，作者提出了相应的解决策略，相当于对整棵树进行了剪枝。

（1）节点赋予重要度指标

模型生成多个解题步骤中存在这个优劣之分，肯定存在更有可能得到正确答案的解题步骤和极小可能得到正确答案的解题步骤。如果对每一种节点都同等看待，将会导致很多冗余搜索。

在这里，作者使用基于值函数的奖励模型计算其对应的奖励值，作为其重要度指标，然后将其转换为其最大可以扩展的节点个数，并对其设置了个数上限和下限，从而防止这个值过大或过小。

（2）减少冗余扩展

当限制了节点的最大孩子个数后，也会出现节点的多个孩子节点对应的解题步骤极度相似的情况。为了进一步缓解这种情况，让模型探索更多的可能性，作者将模型生成的步骤和现有步骤计算相似度，只选择相似度小于一定阈值的步骤进行扩展新节点。

在模拟的过程中，为了进一步增加速度，作者选择了一个较小的模型——Abel-002-7B。

选择最优路径

选择节点的标准是什么？

选择节点基本上使用常规的UCB公式，主要不同在于每个节点奖励的计算方法。这篇论文使用3种常用的奖励策略，分别是基于值函数的、基于过程的奖励模型（PRM）、基于结果的奖励模型（ORM）。

三种奖励模型都是构造了相应的数据，采用常规的方法训练，但没有提节点奖励值具体的计算方式，是直接求和还是带权相加。

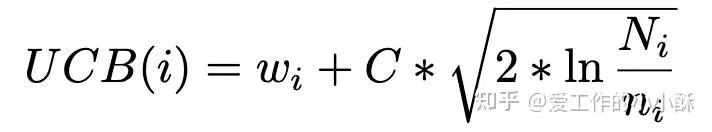
选择每条数据的最优路径的标准是什么？

论文中提到直接使用ORM的结果选择最佳路径。

Self-improving

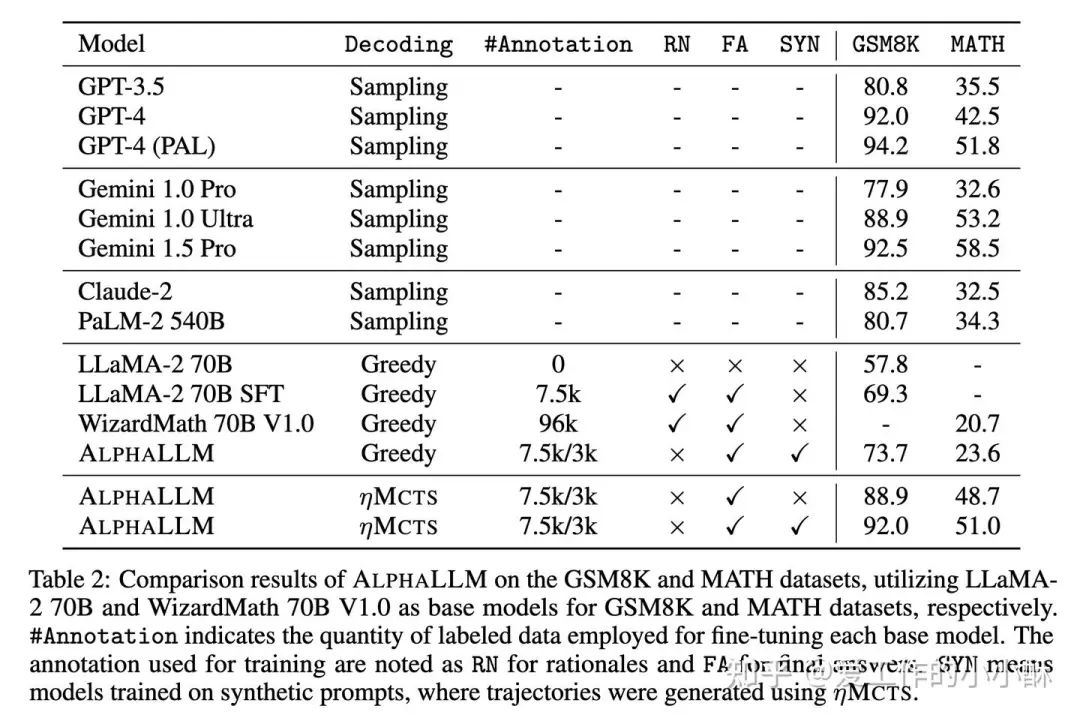
通过上述方式在不同epoch构造相应的数据，使用LLaMA-2 70B 在GSM8K 数据集上训练，使用 Wizardmath 70B V10 在MATH数据集上训练，得到推理能力更强的模型。训练总轮数是3。

指标对比

这个模型的模拟次数很多，但指标上并没有很强。

总结

本篇文章介绍了目前LLM结合MCTS的一些典型方法，从上述文章可以看出，其直接用于优化推理的效果较优，在优化训练的过程中并没有体现出显著优势。

在MCTS的相关设计中，可以看出在结合LLM的过程中，可以跟随问题定义对蒙特卡洛树进行非常独特且多样的改样，例如在叶子节点定义上，从最直观的token级别，到非常启发式的自定义动作空间，并且发现定义越是贴合语言模型本身的能力，越能充分发掘其潜在的能力。

即将迎来新年，回顾过去的一年，感觉自己从各方面都更加成熟了，现在忽然发现原来学习能力的增长可能和成熟度有关，这一年也逐渐找到更优的学习方法。并且一直也在思考自己的各种不足，以及想要学习的技能。最近忽然发现「苏格拉底」式写作方法比较适合人类学习知识，看完这篇文章，你觉得呢？