代码随想录算法训练营第二十一天 | 77. 组合， 216.组合总和III ， 17.电话号码的字母组合

目录

77. 组合

思路

回溯法三部曲

方法一： 回溯未剪枝

方法二：回溯剪枝

心得收获 

216.组合总和III 

思路

方法一：回溯-没有使用sum来统计path里元素的总和

方法二：回溯，使用sum来保存当前路径上的总和

心得收获

17.电话号码的字母组合

思路

数字和字母如何映射

回溯法来解决n个for循环的问题

方法一：回溯

方法二：回溯精简

方法三：回溯精简

 方法四：回溯精简使用列表

心得收获

---

77. 组合

• 题目链接：力扣题目链接

• 文章讲解：代码随想录 

• 视频讲解：带你学透回溯算法-组合问题（对应力扣题目：77.组合），组合问题的剪枝操作

思路

本题是回溯法的经典题目。

直接的解法当然是使用for循环，例如示例中k为2，很容易想到 用两个for循环，这样就可以输出 和示例中一样的结果。

代码如下：

n = 4
for i in range(1,n+1):for j in range(i+1,n+1)print("%d,%d"%(i,j))

输入：n = 100, k = 3 那么就三层for循环，代码如下：

n = 100
for i in range(1,n+1):for j in range(i+1,n+1)for u in range(j+1,n+1):print("%d,%d,%d"%(i,j,u))

如果n为100，k为50呢，那就50层for循环，是不是开始窒息。

此时就会发现虽然想暴力搜索，但是用for循环嵌套连暴力都写不出来！

咋整？

回溯搜索法来了，虽然回溯法也是暴力，但至少能写出来，不像for循环嵌套k层让人绝望。

那么回溯法怎么暴力搜呢？

上面我们说了要解决 n为100，k为50的情况，暴力写法需要嵌套50层for循环，那么回溯法就用递归来解决嵌套层数的问题。

递归来做层叠嵌套（可以理解是开k层for循环），每一次的递归中嵌套一个for循环，那么递归就可以用于解决多层嵌套循环的问题了。

此时递归的层数大家应该知道了，例如：n为100，k为50的情况下，就是递归50层。

一些同学本来对递归就懵，回溯法中递归还要嵌套for循环，可能就直接晕倒了！

如果脑洞模拟回溯搜索的过程，绝对可以让人窒息，所以需要抽象图形结构来进一步理解。

我们在关于回溯算法，你该了解这些！中说到回溯法解决的问题都可以抽象为树形结构（N叉树），用树形结构来理解回溯就容易多了。

那么我把组合问题抽象为如下树形结构：

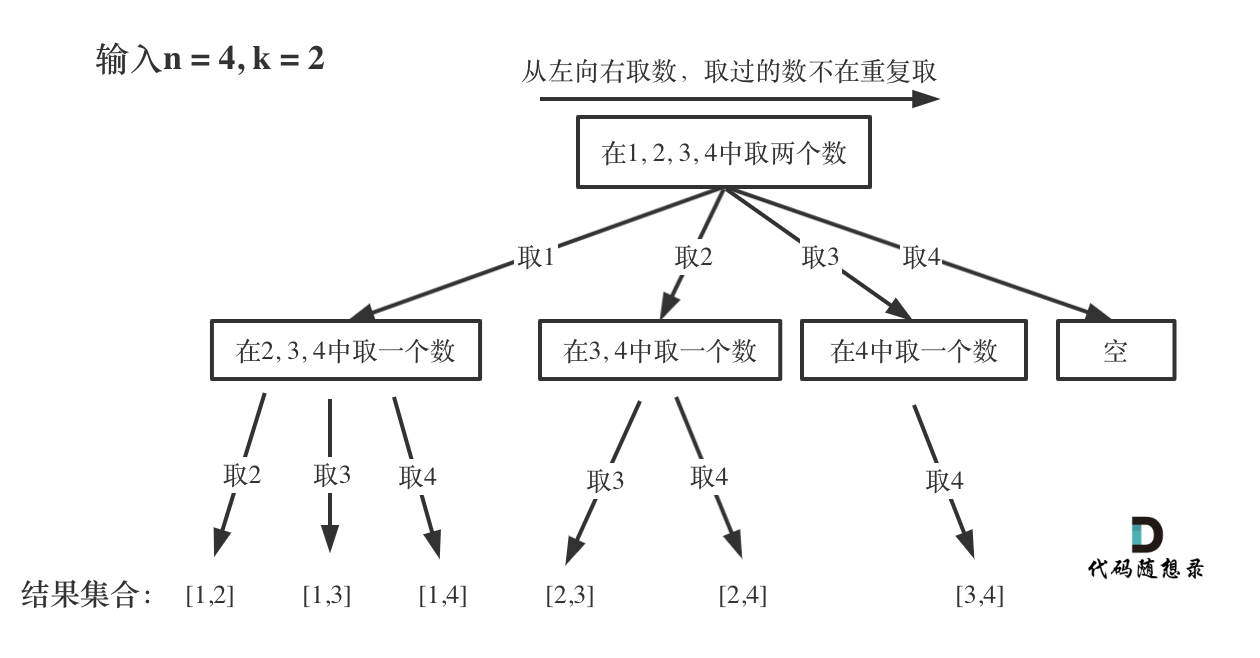
可以看出这棵树，一开始集合是 1，2，3，4， 从左向右取数，取过的数，不再重复取。

第一次取1，集合变为2，3，4 ，因为k为2，我们只需要再取一个数就可以了，分别取2，3，4，得到集合[1,2] [1,3] [1,4]，以此类推。

每次从集合中选取元素，可选择的范围随着选择的进行而收缩，调整可选择的范围。

图中可以发现n相当于树的宽度，k相当于树的深度。

那么如何在这个树上遍历，然后收集到我们要的结果集呢？

图中每次搜索到了叶子节点，我们就找到了一个结果。

相当于只需要把达到叶子节点的结果收集起来，就可以求得 n个数中k个数的组合集合。

在关于回溯算法，你该了解这些！中我们提到了回溯法三部曲，那么我们按照回溯法三部曲开始正式讲解代码了。

回溯法三部曲

• 递归函数的返回值以及参数

在这里要定义两个全局变量，一个用来存放符合条件单一结果path，一个用来存放符合条件结果的集合result。

其实不定义这两个全局变量也是可以的，把这两个变量放进递归函数的参数里，但函数里参数太多影响可读性，所以我定义全局变量了。

函数里一定有两个参数，既然是集合n里面取k个数，那么n和k是两个int型的参数。

然后还需要一个参数，为int型变量startIndex，这个参数用来记录本层递归的中，集合从哪里开始遍历（集合就是[1,...,n] ）。

为什么要有这个startIndex呢？

建议在77.组合视频讲解中，07:36的时候开始听，startIndex 就是防止出现重复的组合。

从下图中红线部分可以看出，在集合[1,2,3,4]取1之后，下一层递归，就要在[2,3,4]中取数了，那么下一层递归如何知道从[2,3,4]中取数呢，靠的就是startIndex。

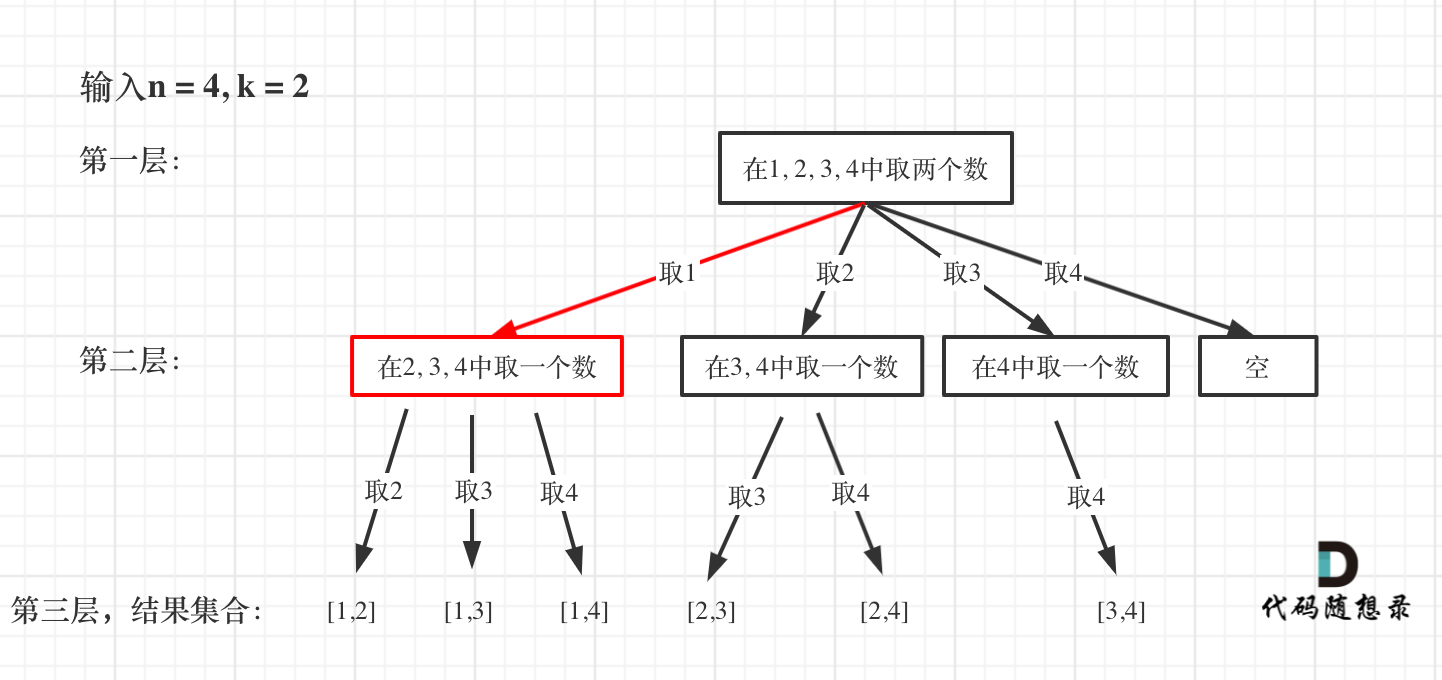
所以需要startIndex来记录下一层递归，搜索的起始位置。

那么整体代码如下：

result = [] // 存放符合条件结果的集合
path = []// 用来存放符合条件单一结果
def backtracking(self,n:int, k:int, startIndex:int)

• 回溯函数终止条件

什么时候到达所谓的叶子节点了呢？

path这个数组的大小如果达到k，说明我们找到了一个子集大小为k的组合了，在图中path存的就是根节点到叶子节点的路径。

如图红色部分：

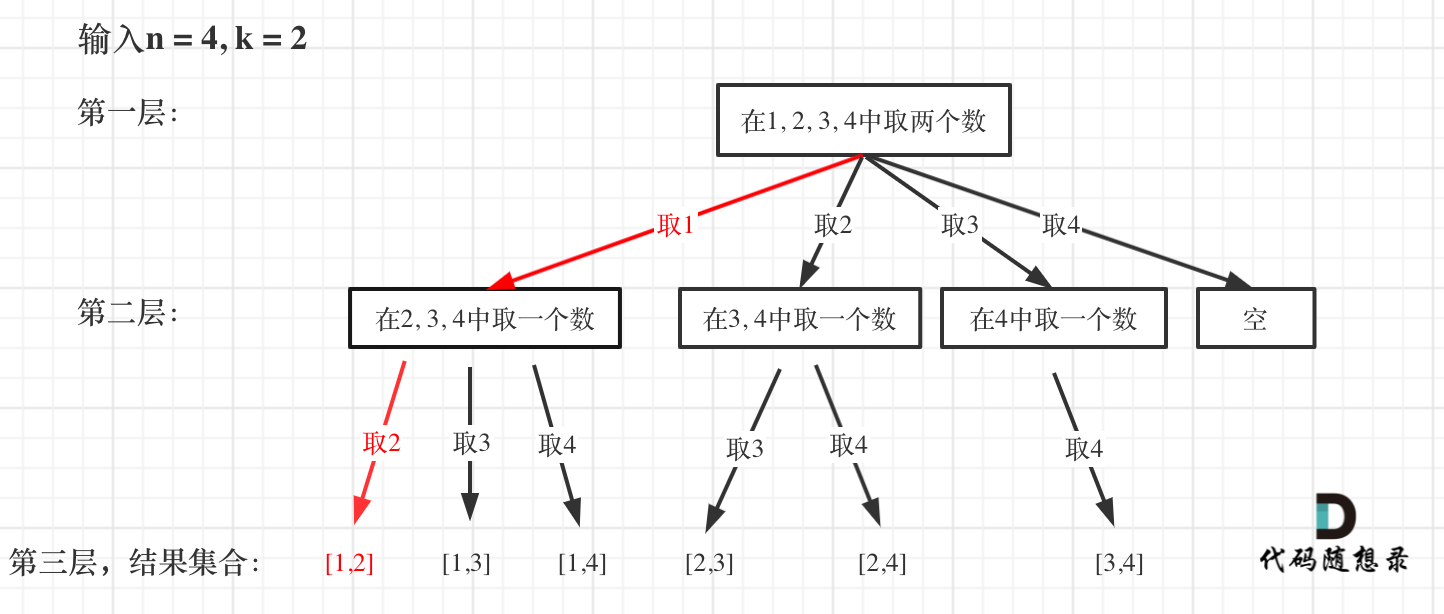
此时用result二维数组，把path保存起来，并终止本层递归。

所以终止条件代码如下：

if len(path) == k:result.append(path[:]) #之前文章里面说过数组传递是引用传递，所以最后的结果可以用浅复制来保存结果，直接用path，会得到空的集合，因为后面path回溯会清空path直接影响到这里return

• 单层搜索的过程

回溯法的搜索过程就是一个树型结构的遍历过程，在如下图中，可以看出for循环用来横向遍历，递归的过程是纵向遍历。

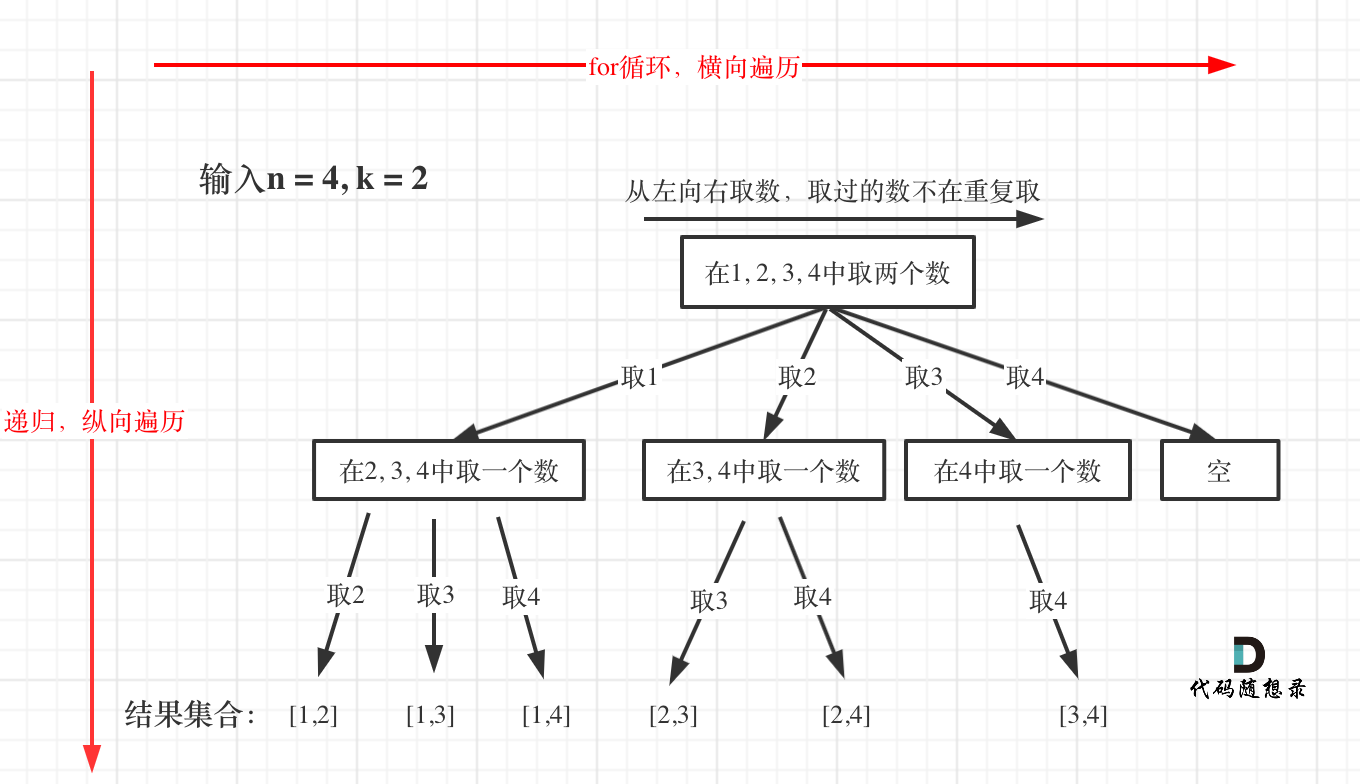
如此我们才遍历完图中的这棵树。

for循环每次从startIndex开始遍历，然后用path保存取到的节点i。

代码如下：

for i in range(startIndex, n + 1):  # 需要优化的地方path.append(i)  # 处理节点self.backtracking(n, k, i + 1, path, result)path.pop()  # 回溯，撤销处理的节点

可以看出backtracking（递归函数）通过不断调用自己一直往深处遍历，总会遇到叶子节点，遇到了叶子节点就要返回。

backtracking的下面部分就是回溯的操作了，撤销本次处理的结果。

方法一： 回溯未剪枝

class Solution:def combine(self, n: int, k: int) -> List[List[int]]:result = []  # 存放结果集self.backtracking(n, k, 1, [], result)return resultdef backtracking(self, n, k, startIndex, path, result):if len(path) == k:result.append(path[:])returnfor i in range(startIndex, n + 1):  # 需要优化的地方path.append(i)  # 处理节点self.backtracking(n, k, i + 1, path, result)path.pop()  # 回溯，撤销处理的节点

方法二：回溯剪枝

class Solution:def combine(self, n: int, k: int) -> List[List[int]]:result = []  # 存放结果集self.backtracking(n, k, 1, [], result)return resultdef backtracking(self, n, k, startIndex, path, result):if len(path) == k:result.append(path[:])returnfor i in range(startIndex, n - (k - len(path)) + 2):  # 优化的地方path.append(i)  # 处理节点self.backtracking(n, k, i + 1, path, result)path.pop()  # 回溯，撤销处理的节点

心得收获 

回溯本身是暴力解法，但是有时候也是可以剪枝优化的

在遍历的过程中有如下代码：

for i in range(startIndex, n + 1):  # 需要优化的地方path.append(i)  # 处理节点self.backtracking(n, k, i + 1, path, result)path.pop()  # 回溯，撤销处理的节点

这个遍历的范围是可以剪枝优化的，怎么优化呢？

来举一个例子，n = 4，k = 4的话，那么第一层for循环的时候，从元素2开始的遍历都没有意义了。 在第二层for循环，从元素3开始的遍历都没有意义了。

这么说有点抽象，如图所示：

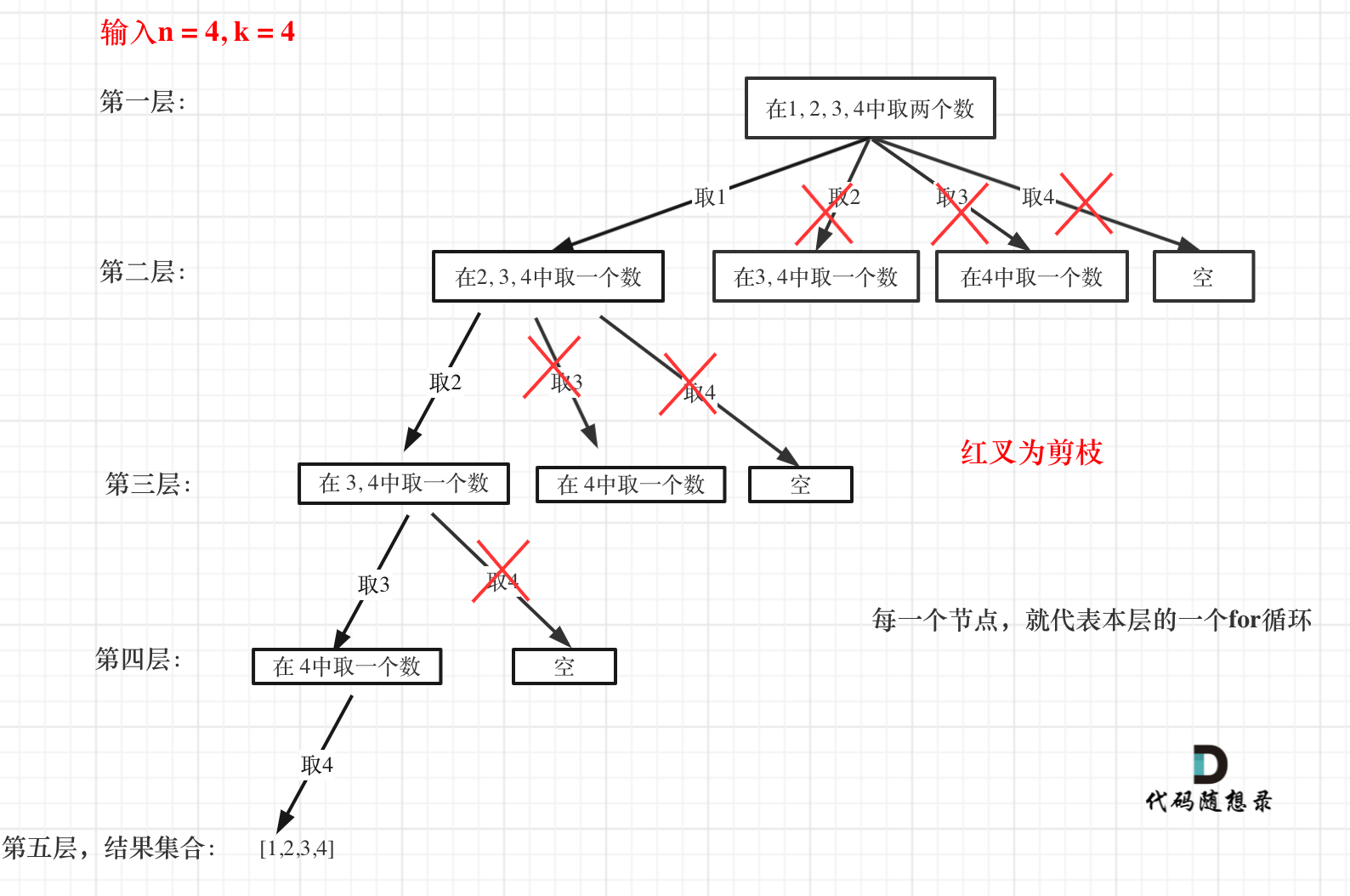
图中每一个节点（图中为矩形），就代表本层的一个for循环，那么每一层的for循环从第二个数开始遍历的话，都没有意义，都是无效遍历。

所以，可以剪枝的地方就在递归中每一层的for循环所选择的起始位置。

如果for循环选择的起始位置之后的元素个数 已经不足 我们需要的元素个数了，那么就没有必要搜索了。

注意代码中i，就是for循环里选择的起始位置。

for i in range(startIndex, n + 1):

接下来看一下优化过程如下：

1. 已经选择的元素个数：len(path);

2. 所需需要的元素个数为: k - len(path);

3. 列表中剩余元素（n-i） >= 所需需要的元素个数（k - len(path)）

4. 在集合n中至多要从该起始位置 : i <= n - (k - len(path)) + 1，开始遍历

为什么有个+1呢，因为包括起始位置，我们要是一个左闭的集合。

举个例子，n = 4，k = 3， 目前已经选取的元素为0（len(path)为0），n - (k - 0) + 1 即 4 - ( 3 - 0) + 1 = 2。

从2开始搜索都是合理的，可以是组合[2, 3, 4]。

这里大家想不懂的话，建议也举一个例子，就知道是不是要+1了。

由于python中range函数是左闭右开的区间，所以还需要再+1，才是真正需要的集合

所以优化之后的for循环是：

for i in range(startIndex, n - (k - len(path)) + 2): 

216.组合总和III 

• 题目链接：力扣题目链接

• 文章讲解：代码随想录 

• 视频讲解：和组合问题有啥区别？回溯算法如何剪枝？| LeetCode：216.组合总和III

思路

该题目和组合题目的思路大致相同，但是多了一个限制条件

方法一：回溯-没有使用sum来统计path里元素的总和

class Solution:def combinationSum3(self, k: int, n: int) -> List[List[int]]:result = []path = []self.backtracking(n,k,1,path,result)return resultdef backtracking(self,n,k,startIndex,path,result) -> None:if sum(path) > n:returnif len(path) == k :if sum(path) == n:result.append(path[:]) returnfor i in range(startIndex,9-(k-len(path))+2):path.append(i)self.backtracking(n,k,i+1,path,result)path.pop()

方法二：回溯，使用sum来保存当前路径上的总和

class Solution:def combinationSum3(self, k: int, n: int) -> List[List[int]]:result = []  # 存放结果集self.backtracking(n, k, 0, 1, [], result)return resultdef backtracking(self, targetSum, k, currentSum, startIndex, path, result):if currentSum > targetSum:  # 剪枝操作return  # 如果path的长度等于k但currentSum不等于targetSum，则直接返回if len(path) == k:if currentSum == targetSum:result.append(path[:])returnfor i in range(startIndex, 9 - (k - len(path)) + 2):  # 剪枝currentSum += i  # 处理path.append(i)  # 处理self.backtracking(targetSum, k, currentSum, i + 1, path, result)  # 注意i+1调整startIndexcurrentSum -= i  # 回溯path.pop()  # 回溯

心得收获

明明python中int变量是不可变类型，在改变了currentSum的值之后，currentSum会指向新的地址，不会影响到上一层递归的currentSum值，那解法二中为什么currentSum要做回溯呢？ 

其实大家可以debug一下，currentSum确实是不影响上一层递归的值，可以看下图示例：

17.电话号码的字母组合

• 题目链接：力扣题目链接

• 文章讲解：代码随想录 

• 视频讲解：还得用回溯算法！| LeetCode：17.电话号码的字母组合

思路

理解本题后，要解决如下三个问题：

1. 数字和字母如何映射
2. 两个字母就两个for循环，三个字符我就三个for循环，以此类推，然后发现代码根本写不出来
3. 输入1 * #按键等等异常情况

数字和字母如何映射

可以使用map或者定义一个一维数组来做映射，我这里定义一个一维数组，代码如下：

        self.letterMap = ["",     # 0"",     # 1"abc",  # 2"def",  # 3"ghi",  # 4"jkl",  # 5"mno",  # 6"pqrs", # 7"tuv",  # 8"wxyz"  # 9]

回溯法来解决n个for循环的问题

对于回溯法还不了解的同学看这篇：关于回溯算法，你该了解这些！

例如：输入："23"，抽象为树形结构，如图所示：

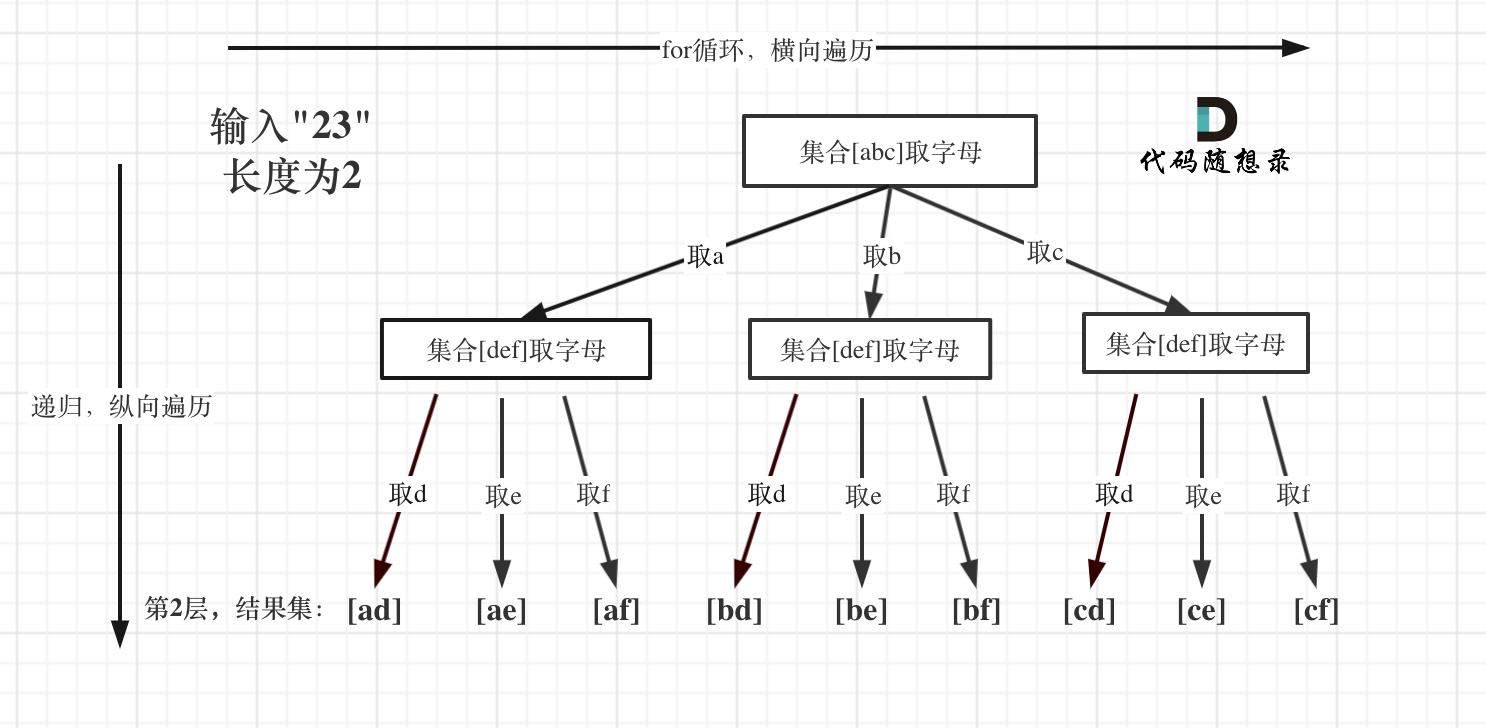
图中可以看出遍历的深度，就是输入"23"的长度，而叶子节点就是我们要收集的结果，输出["ad", "ae", "af", "bd", "be", "bf", "cd", "ce", "cf"]。

回溯三部曲：

• 确定回溯函数参数

首先需要一个字符串s来收集叶子节点的结果，然后用一个字符串数组result保存起来，这两个变量我依然定义为全局。

再来看参数，参数指定是有题目中给的string digits，然后还要有一个参数就是int型的index。

注意这个index可不是 77.组合 和216.组合总和III中的startIndex了。

这个index是记录遍历第几个数字了，就是用来遍历digits的（题目中给出数字字符串），同时index也表示树的深度。

• 确定终止条件

例如输入用例"23"，两个数字，那么根节点往下递归两层就可以了，叶子节点就是要收集的结果集。

那么终止条件就是如果index 等于 输入的数字个数（digits.size）了（本来index就是用来遍历digits的）。

然后收集结果，结束本层递归。

代码如下：

if index == len(digits):self.result.append(self.s)return

• 确定单层遍历逻辑

首先要取index指向的数字，并找到对应的字符集（手机键盘的字符集）。

然后for循环来处理这个字符集，代码如下：

letters = self.letterMap[int(digits[index])]
for i in letters:self.s += iself.backtracking(digits,index+1)self.s = self.s[:-1]

注意这里for循环，可不像是在回溯算法：求组合问题！和回溯算法：求组合总和！中从startIndex开始遍历的。

因为本题每一个数字代表的是不同集合，也就是求不同集合之间的组合，而77. 组合 和216.组合总和III 都是求同一个集合中的组合！

注意：输入1 * #按键等等异常情况

代码中最好考虑这些异常情况，但题目的测试数据中应该没有异常情况的数据，所以我就没有加了。

但是要知道会有这些异常，如果是现场面试中，一定要考虑到！

方法一：回溯

class Solution:def __init__(self) -> None:self.letterMap = ["",     # 0"",     # 1"abc",  # 2"def",  # 3"ghi",  # 4"jkl",  # 5"mno",  # 6"pqrs", # 7"tuv",  # 8"wxyz"  # 9]self.result = []self.s = ""def letterCombinations(self, digits: str) -> List[str]:if len(digits) < 1: return self.resultself.backtracking(digits,0)return self.resultdef backtracking(self,digits,index) -> None:if index == len(digits):self.result.append(self.s)returnletters = self.letterMap[int(digits[index])]for i in letters:self.s += iself.backtracking(digits,index+1)self.s = self.s[:-1]

方法二：回溯精简

class Solution:def __init__(self):self.letterMap = ["",     # 0"",     # 1"abc",  # 2"def",  # 3"ghi",  # 4"jkl",  # 5"mno",  # 6"pqrs", # 7"tuv",  # 8"wxyz"  # 9]self.result = []def getCombinations(self, digits, index, s):if index == len(digits):self.result.append(s)returndigit = int(digits[index])letters = self.letterMap[digit]for letter in letters:self.getCombinations(digits, index + 1, s + letter)def letterCombinations(self, digits):if len(digits) == 0:return self.resultself.getCombinations(digits, 0, "")return self.result

方法三：回溯精简

class Solution:def __init__(self):self.letterMap = ["",     # 0"",     # 1"abc",  # 2"def",  # 3"ghi",  # 4"jkl",  # 5"mno",  # 6"pqrs", # 7"tuv",  # 8"wxyz"  # 9]def getCombinations(self, digits, index, s, result):if index == len(digits):result.append(s)returndigit = int(digits[index])letters = self.letterMap[digit]for letter in letters:self.getCombinations(digits, index + 1, s + letter, result)def letterCombinations(self, digits):result = []if len(digits) == 0:return resultself.getCombinations(digits, 0, "", result)return result

 方法四：回溯精简使用列表

class Solution:def __init__(self):self.letterMap = ["",     # 0"",     # 1"abc",  # 2"def",  # 3"ghi",  # 4"jkl",  # 5"mno",  # 6"pqrs", # 7"tuv",  # 8"wxyz"  # 9]def getCombinations(self, digits, index, path, result):if index == len(digits):result.append(''.join(path))returndigit = int(digits[index])letters = self.letterMap[digit]for letter in letters:path.append(letter)self.getCombinations(digits, index + 1, path, result)path.pop()def letterCombinations(self, digits):result = []if len(digits) == 0:return resultself.getCombinations(digits, 0, [], result)return result

心得收获