【深度学习与大模型基础】第9章-条件概率以及条件概率的链式法则

简单理解条件概率

条件概率就是在已知某件事发生的情况下，另一件事发生的概率。用数学符号表示就是：
P(A|B) = 在B发生的前提下，A发生的概率。

计算机例子：垃圾邮件过滤

假设你写了一个程序来自动判断邮件是否是垃圾邮件（Spam）。已知：

所有邮件中，20%是垃圾邮件（P(Spam) = 0.2）。
垃圾邮件中，50%包含“免费”这个词（P(Free|Spam) = 0.5）。
正常邮件中，只有10%包含“免费”（P(Free|¬Spam) = 0.1）。

现在问题是：如果一封邮件包含“免费”，它是垃圾邮件的概率是多少？
也就是求 P(Spam|Free)。

如何计算？

根据条件概率公式：P(A|B)=P(A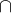 $\cap$ B)/P(B)

即有：

分子：垃圾邮件中带“免费”的概率 × 垃圾邮件的概率
= 0.5 × 0.2 = 0.1
分母：所有带“免费”的邮件的概率（包括垃圾和正常邮件）
= P(Free|Spam)P(Spam) + P(Free|¬Spam)P(¬Spam)
= 0.5×0.2 + 0.1×0.8 = 0.1 + 0.08 = 0.18

所以：

结论

即使“免费”在垃圾邮件中更常见，但因为正常邮件基数大，实际包含“免费”的邮件是垃圾邮件的概率只有约55.6%。这就是条件概率的直观体现——它结合了先验知识（垃圾邮件的比例）和新证据（“免费”这个词）。

应用场景

推荐系统：已知用户喜欢游戏（B），那么推荐显卡（A）的概率是多少？
故障诊断：如果电脑蓝屏（B），是内存故障（A）的概率有多大？
语音识别：在当前上下文（B）下，下一个词是“苹果”（A）的概率是多少？

条件概率帮助计算机在不确定性的世界中做出更聪明的决策！

使用python实现在当前上下文（B）下，下一个词是“苹果”（A）的概率是多少的代码

1.安装NLTK
pip install nltk

下载附件分词模型文件tokenizers.zip解压到 D:\nltk_data

3..实现在当前上下文（B）下，下一个词是“苹果”（A）的概率是多少的代码

import nltk
nltk.download('punkt')  # 确保punkt已下载
nltk.download('punkt_tab')
from nltk import bigrams, FreqDist
from nltk.tokenize import word_tokenize# 示例文本（中文需提前分词，英文可直接tokenize）
text = "吃 苹果 买 苹果 吃 香蕉 买 手机"  # 中文示例（已分词）
tokens = word_tokenize(text)  # 分词
bigram_pairs = list(bigrams(tokens))  # 生成连续词对# 统计条件概率
context = "吃"
next_word = "苹果"
count_apple = sum(1 for (prev, curr) in bigram_pairs if prev == context and curr == next_word)
total_context = sum(1 for (prev, curr) in bigram_pairs if prev == context)
p_apple_given_context = count_apple / total_context if total_context > 0 else 0print(f"P('{next_word}'|'{context}') = {p_apple_given_context:.2f}")

条件概率的链式法则。基础概念

条件概率：比如事件B发生的条件下，事件A发生的概率，记作 P(A∣B)。
- 例子：明天降雨的概率是 P(雨)，但如果今天乌云密布（B），那么明天降雨的概率会变，即 P(雨∣乌云)。
链式法则：把多个条件的联合概率拆解成一步步的条件概率相乘。
- 公式：
  P(A $\cap$ B $\cap$ C)=P(A)⋅P(B∣A)⋅P(C∣A $\cap$ B)
- 意思是"A、B、C同时发生"的概率，等于：
  1. 先发生A的概率 P(A)，
  2. 在A发生下B的概率 P(B∣A)，
  3. 在A和B都发生下C的概率 P(C∣A $\cap$ B)。

应用场景

假设我们要预测一段文本是否是垃圾邮件（Spam），文本中有两个单词："免费"和"赢"。

联合概率：
计算 P(免费 $\cap$ 赢 $\cap$ Spam)（即“免费”和“赢”同时出现且是垃圾邮件的概率）。
链式法则拆解：
P(免费赢Spam)=P(Spam)⋅P(免费∣Spam)⋅P(赢∣免费Spam)
1. 先算垃圾邮件的概率 P(Spam)，
2. 在垃圾邮件中，“免费”出现的概率 P(免费∣Spam)，
3. 在垃圾邮件且已有“免费”时，“赢”出现的概率 P(赢∣免费 $\cap$ Spam)。

3. 为什么有用？

简化复杂问题：直接算联合概率很难，但拆成条件概率后，可以通过数据统计（比如数邮件中出现单词的次数）来估算。
贝叶斯网络的基础：链式法则是图模型（如贝叶斯网络）的核心，用来描述变量间的依赖关系。

python实现

假设我们要预测一段文本是否是垃圾邮件（Spam），文本中有两个单词："免费"和"赢"。
计算 P(免费,赢,Spam)（即“免费”和“赢”同时出现且是垃圾邮件的概率）

import pandas as pd# 模拟数据：每封邮件的文本和标签（1=Spam, 0=Not Spam）
data = {"text": ["免费 赢 大奖",        # Spam"免费 参加 活动",      # Spam"赢 免费 门票",        # Spam"明天 开会",           # Not Spam"请 回复 邮件"         # Not Spam],"label": [1, 1, 1, 0, 0]
}df = pd.DataFrame(data)
print(df)# 计算 P(Spam)
total_emails = len(df)
spam_emails = df[df["label"] == 1]
p_spam = len(spam_emails) / total_emails# 计算 P(免费|Spam): 垃圾邮件中包含"免费"的概率
spam_with_free = spam_emails[spam_emails["text"].str.contains("免费")]
p_free_given_spam = len(spam_with_free) / len(spam_emails)# 计算 P(赢|免费, Spam): 在垃圾邮件且含"免费"时，同时含"赢"的概率
spam_free_with_win = spam_with_free[spam_with_free["text"].str.contains("赢")]
p_win_given_free_spam = len(spam_free_with_win) / len(spam_with_free) if len(spam_with_free) > 0 else 0# 联合概率: P(免费, 赢, Spam) = P(Spam) * P(免费|Spam) * P(赢|免费, Spam)
joint_probability = p_spam * p_free_given_spam * p_win_given_free_spamprint(f"P(Spam): {p_spam:.2f}")
print(f"P(免费|Spam): {p_free_given_spam:.2f}")
print(f"P(赢|免费, Spam): {p_win_given_free_spam:.2f}")
print(f"联合概率 P(免费, 赢, Spam): {joint_probability:.4f}")