题意：给一个轮盘，或者说序列，有两个操作
1.随意旋转，类似于下标0 1 2 3 4（初始下标）变成 3 4 0 1 2
2.为上面添加相应位置的值0 0 0 0 0（初始值）变成 0 1 2 3 4
起始值均为0，问给出一个最终结果序列，能从初始值到达吗？
初始值均为0，初始序列和结果序列长度均为n
思路：
没得说，先玩一下序列，或者说打个表，对结果有个判断，这里并不对这个结果的过程在提及了，直接说结论
结论：
先看轮盘不动的情况（样例只用n==5），首先你会发现当操作数达到n次之后，就会还原，为啥？
| 下标 | 0 | 1 | 2 | 3 | 4 |
| 大小 | 5*k%n | 1*k%n | 2*k%n | 3*k%n | 4*k%n |
操作n次之后必然被取余回全体为0（下标0为了后续方便理解设置成了+5，毕竟效果是一样的）
接下来带上旋转，然后在这里我们先只讨论下标1和下标2
根据这个计算方式，我们设当前下标的轮盘内容，设下标1为a，按照上面你自己旋转试试，无论你把谁转到当前位置，都是这个效果： (因为取余的存在，你可以把5*k也看成0*k，方便于这个思路的理解)
| 下标 | 1 | 2 |
| 大小 | a(0,1,2,3,4) | a+1(1,2,3,4,5) |
所以轮盘的旋转并不影响两个值之间的差值，b[p]-b[p-1]的差值一定代表了操作数，因为是等差数列，a0=0,k=1；
那么回到整体数字的改变是怎么来的？他可以是经过多次旋转得到的，但是根据上面你能发现可以归结到一个公式
S=( a*(k-1)%n + (a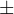 
p) )%n
k是最终转动轮数，p是旋转一次轮盘会造成值的偏移
旋转，可以看成在原本增加值的基础上减少或增加了某个值，你之前的多次旋转最终都会被%n，偏移值造成的影响始终超不过n，同时轮盘可以旋转出n种情况（p的值就是0-4），也就是如果你多次旋转造成的p的影响，其实都可以用一次旋转来成功得到。
那么至此思路非常明确，因为等差数列的特性能计算出数值的增加次数，下标0位置是否是0代表需不需要一个p来让结果序列偏移。
代码：
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define endl '\n'
#define IOS ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
const int N = 1e6+10;
const int INF = 1e12;
const int MOD = 998244353;void solve(){int n;cin >> n;vector<int> ve(n+10);set<int> se;for(int i=0;i<n;i++){cin >> ve[i];if(i){se.insert( (ve[i]-ve[i-1]+n)%n );}}se.insert( (ve[0]-ve[n-1]+n)%n );if(se.size()!=1) cout << -1 << endl;else if(*se.begin()==0) cout << ((ve[0]==0)?0:n+1) << endl;else cout << *se.begin()+(ve[0]!=0) << endl;
}signed main() {IOS;int t = 1;
// cin >> t;while (t--) {solve();}}
