7. 第七章 迭代

7. 迭代

本章讲关于迭代的话题, 得带即重复运行一段代码语句块的能力.
我们在5.8节中见过一种递归来进行迭代, 在4.2节中见过另一种使用for循环进行的迭代.
在本章中我们会将看到使用while循环进行的第三种迭代.
首先我们先进一步讲讲变量赋值的话题.

7.1 重新赋值

对一个变量进行多次赋值是合法的. 你的赋值语句使现有的变量引用一个新值(并不再引用老值).

>>> x = 4
>>> x
5
>>> x = 7
x
7

因为第一次显示x时, 它的值是5, 而第二次时它的值是7.
下图显示了在状态图中, 重新赋值是什么样子的.

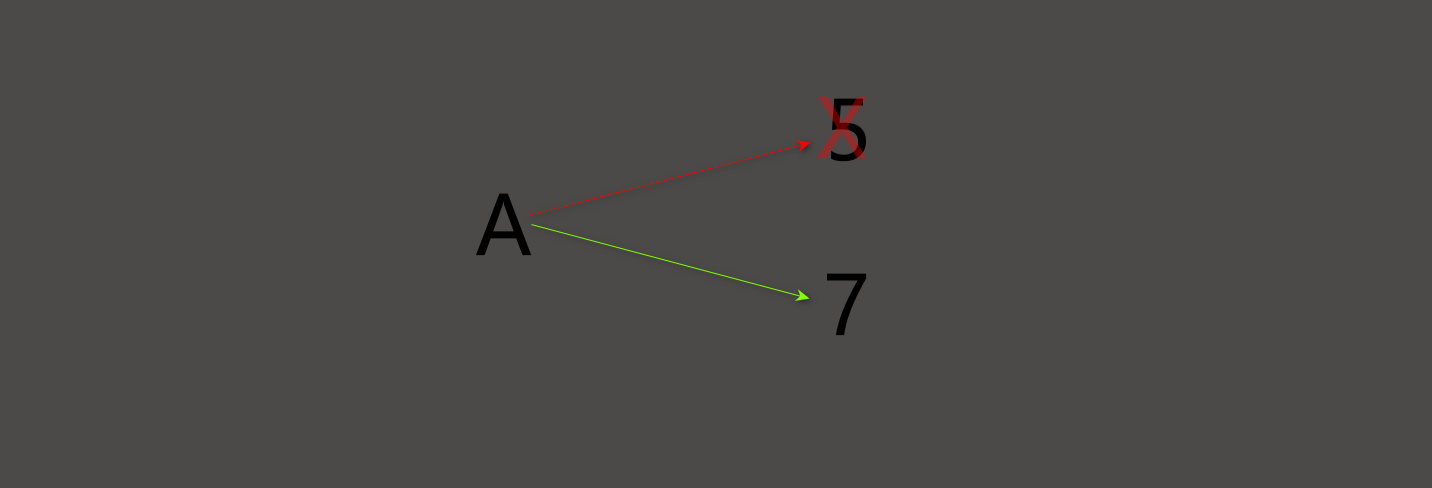
注意一个常见的误区: Python中使用等号(=)来表示赋值, 故很容易将a=b这样的赋值语句理解成数学中的等式.
相等判断是个对称关系, 而赋值并不是, 例如:
在数学中, 如果a=7, 那么7=a. 但在Python中, 语句a=7是合法的, 但7=a则是非法的.
另外, 在数学中, 一个相等判断的命题总是非真即假. 如果现在a=b, 那么a总会等于b.
在Python中, 赋值语句会让两个变量变得相等, 但它们并不会总保持那个状态:

>>> a = 5
>>> b = a   # a和b现在相等.
>>> a = 3	# a和b不再相等.
>>> b
5

第三行修改a的值, 但不并不会修改b的值, 所有它们不再相等.
虽然重新赋值常常哼有用处, 但是因该谨慎使用.
如果变量的值经常变化, 会导致程序难以阅读和调试.

7.2 更新变量

重新赋值的最常见形式是更新, 此时变量的新值依赖于旧值.

>>> x = x + 1

这个语句的意思是'获取x的当前值, 加1, 再更新x为此新值'.
如果尝试更新一个并不存在的变量, 则会得到错误, 
因为Python在赋值给x之前会先计算等号右边的部分:

>>> x = x + 1
Traceback (most recent call last):File "<stdin>", line 1, in <module>
NameError: name 'x' is not defined

在更新变量之前, 必须对它进行初始化.
通常通过一个简单赋值操作来进行初始化:

>>> x = 0
>>> x = x + 1
>>> x
1

通过加1来更新一个变量, 称为增量(increment); 减1的操作成为减量(decrement).

7.3 while 语句

计算机常被用来自动化重复处理某些任务.
重复执行相同或相似的任务, 而不犯错误, 这是计算机所擅长于人之处.
在计算机程序中, 重复也被称为迭代.我们之前已经看到两个函数countdown和print_n, 它们使用递归来进行迭代操作.
由于迭代如此常见, Python提供了语言特性来支持它.
其中一个是我们在4.2节中见过的for语句. 后面我们会再回到这个话题.另一个则是while语句. 下面是使用while语句实现的countdown函数:

def countdown(n):while n > 0:print(n)n = n - 1print('Blastoff!')

你基本上可以按照英语来理解while语句. 它的意思是:
'每当n还大于0时, 显示n的值, 并将n减1. 当n变成0的时候, 显示单词Blastoff!.'用更正确的说法, 下面是while语句的执行流程.
1. 确认条件是真还是假.
2. 如果条件为假, 退出while语句.
3. 如果条件为真, 则运行while语句的语句体, 并返回第1步.这种类型的流程成为循环(loop), 因为第3步又循环返回到最顶端的第一步了.
循环语句体里面应当修改一个或多个变量的值, 以致循环的条件最终能变成假, 而退出循环.
否则这个循环会永远重复下去, 这样的情况成为无限循环.
计算机科学家在读到洗发液的说明'涂抹, 冲洗, 重复'时, 总会感到有趣, 因为这是一个无限循环.在conutdown这个例子里, 我们可以正确循环必然终结: 如果n是0或负数, 该函数从不运行.
否则, n的值都会减小, 因此最终n会变成0.对于某些循环, 就并不一定那么容易判断了. 例如:

def sequence(n):while n != 1:print(n)# n是偶数if n % 2 == 0:n = n / 2# n是偶数else:n = n * 3 + 1sequence(3)

# 运行终端显示:
3
10
5.0
16.0
8.0
4.0
2.0

这个循环的条件是n != 1, 所有只要n还没有变成1而导致添加变假, 循环就会一直进行下去.
每个循环中, 程序输出n的值, 并检测它是偶数还是奇数. 
如果是偶数, n会除以2.
如果是奇数, n会被替换为n * 3 + 1.
例如, 如果传入sequence函数的参数是3, 则n的结果值是: 3, 10, 5, 16, 8, 4, 2, 1.

因为n有时候增加, 有时候减少, 没有办法找到明显证据确定n一定最终变成1, 或者说程序会终止.
对于某些特定的n值, 我们可以证明最终会终止.
例如, 如果开始的参数是2的幂方, 则每次循环n都是偶数, 直到变成1.
前面的例子中有一部分就是这样的序列, 以16开始.但困难的问题是, 我们是或否能够证明这个程序所有的正值都最终终止.
至今为止, 还没有人对这个问题给出证明或证伪.
(参见http://en.wikipedia.org/wiki/Collatz_conjecture)

作为练习, 重写5.8节中的print_n函数, 使用循环而非递归来实现.

# 5.8节中的print_n函数
def print_n(s, n):if n <= 0:returnprint(s)print_n(s, n - 1)print_n('s', 4)

# while循环重写方案.
def print_n(s, n):while n > 0:print(s)n = n - 1print_n('s', 4)

7.4 break语句

有时候只有在循环语句体中执行途中才能知道是不是到了退出循环的时机.
这时候可以使用break语句来跳出循环.
例如, 假设你想要获得用户输入, 直到他们输入done. 可以这么写:

while True:line = input('输入>:')if line =='done':breakprint(line)print('Done!')

 循环的条件是True, 总是为真, 所以循环会一直运行, 直到遇到break语句.每次循环之内, 都会先用一个(输入>:)来提示用户输入. 如果用户输入done, break语句会退回循环.否则程序会显示用户输入的内容, 并重新回到循环的顶端.这里是一个运行的实例:

# 输入什么, 打印什么.
> not done
not done
# 输入done, 跳出循环.
> done
Done!

这种写while循环的方式很常见, 
因为可以把判断循环的逻辑放在循环中的任何地方(而不只是在顶端),
并且可以以肯定的语气来表示终结条件('当这样发生时停止循环'), 
而不是否定的语句('继续执行, 直到那个条件发生').

7.5 平方根

程序中常常使用循环来进行数值计算, 以一个近似值开始, 并迭代地优化计算结果.
例如, 计算平方根的方法之一是牛顿方法. 假设你想要知道a的平方根.
如果你可以任意一个估算值x开始, 可以使用如下的方程获取得一个更好的估计值.
y = (x + a/x) / 2
例如, 如果a是4, 而x是3:

>>> a = 4
>>> x = 3
>>> y = (x + a / x) / 2
>>> y
2.1666666666666665

这个结果更接近正确的答案(√4 = 2, √根号). 如果我们使用新的估计值重复这个过程, 会得到更近似的结果:

>>> x = y
>>> y = (x + a / x) / 2
>>> y 
2.0064102564102564

在经过几次重复更新, 估计值会几乎完全准确:

>>> x = y
>>> y = (x + a / x) / 2
>>> y
2.0000102400262145>>> x = y
>>> y = (x + a / x) / 2
>>> y
2.0000000000262146

通常来说, 我们并不能提前知道需要多少步才能得到正确的答案, 
但是估计值不再发生变化时, 我们就知道达到目的了.

>>> x = y
>>> y = (x + a / x) / 2
>>> y
2.0>>> x = y
>>> y = (x + a / x) / 2
>>> y
2.0

当y == x时, 可以终止, 下面是一个以估计值x开始, 并不断迭代优化直到它不再变化的循环:

a = 4
x = 3while True:print(x)y = (x + a / x) / 2# 当x已经是2.0, 再次计算y的值还是2.0 则退出循环.if y == x:breakx = y

对多数的a值来说, 这样的效果很好, 但通常来说, 测试float的相等是危险的.
浮点数只是近似正确: 大部分有理数, 如1/3, 以及无理数, 如√2, 都不能用float精确表示.
比起判断x和y是否精确相等, 更安全的方式是利用内置函数abs来计算它们之间差值的绝对值, 或者说量级:

if abs(y - x) < epsilon:break

这里的epsilon的值是0.0000001, 用来决定近视度是足够的.

测试浮点数的相等性可以很危险:
因为浮点数在计算机中的存储和运算方式可能会导致精度丢失, 从而影响比较结果.在计算机中, 浮点数是以二进制形式存储的, 但某些浮点数无法准确表示为二进制数字.
例如, 0.1在二进制中是一个无限循环的数字. 这样的表示问题会导致一些计算结果不准确.因此, 在比较两个浮点数时不能简单地使用'=='操作符进行比较,
因为即使两个数看起来相等, 它们在计算机内部的存储方式可能不同, 因此比较的结果可能是错误的。解决这个问题的一种常见方法是, 将两个浮点数相减, 然后检查它们的差异是否小于某个非常小的数值阈值.
例如, 可以比较两个浮点数的差异是否小于0.0001.另外, 有些编程语言提供了特殊的函数或库来处理浮点数的比较问题.
例如Python中的math.isclose()函.
使用这些函数可以更加可靠地比较浮点数的相等性.

7.6 算法

牛顿方法是算法的一个例子: 它是解决一类问题的机械化过程(在这个例子里, 问题是计算平方根.)
要理解算法是什么, 从一个算不上算法的东西开始可能更简单.
在学习个位数相乘时, 你可能背诵乘法表. 实际上, 你记住了100个特别的答案, 这种知识不算是算法.
但是, 如果你比较'懒', 可能已经学会了一些小技巧来偷懒. 
例如, 要计算n和9的乘积, 你可能写下n-1作为十位数, 10-n作为个位数.
8 * 9 , n是8, n-1=7 作为十位数, 10-8=2 作为个数数, 结果为72.
这个小技巧是计算任意个人数和9的乘积的通用方法. 这算是一个算法.

相似地, 你学过的进位加法, 借位减法以及长除法都是算法.
算法的特点之一是它们不需要任何聪明才智就能执行.
它们是一个机械化的过程, 其中每一步都依照一组简单的规则接着上一步进行.执行算法非常枯燥, 但设计算法的过程却充满趣味和智力挑战, 并且是计算机科学家的一个核心部分.
一些人们自然而然, 汉武困难或者下意识所做的事情, 用算法表达却最为困难.
理解自然语言是一个好例子, 我们都能理解自然语言, 但是至今为止还没有人能解释我们怎么做到的,
至少没办法用算法解释.

7.7 调试

当你开始编写更大的程序时, 常常会发现自己花费更多的时间用于调试.
更多的代码意味着更多的出现机会, 以及更多可能隐藏着bug的地方.
削减调用时间的方法之一是'二分调试'(debugging by bisection). 
例如, 如果你的程序有100行代码, 如果每次检测一行, 需要100步.想反地, 可以尝试把问题分成两半. 找打程序的中点, 或者接近那里的地方, 找一个可以检查效果的代码.
添加print语句(或者其他的可以有检测效果的代码)并运行程序.
如果中点检验的结果是错误的, 说明错误必然出现在程序的前半部分.
如果是正确的, 那错误则在程序的后半部分.每进行一次这样的检查, 就减少了一半需要检查的代码.
经过6步之后(显然少于100步), 就能够减少到一致两行代码, 至少理论上如此. 

实践中, 常常很难确定'程序的中点'在哪里, 并且并不总是能够检验它.
通过数代码的行数来确定中点显然没有意义.
相反地, 思考程序中哪些地方可能出错, 哪些地方容易加上一个检查.
然后选择一个你认为在其前后发生错误概率差不多的点进行检查.

7.8 术语表

重新赋值(reassignment): 对一个已经存在的变量赋予一个新值.更新(update): 一种赋值操作, 新值依赖一变量的旧值.初始化(initialization): 一种赋值操作, 给变量一个初始的值, 以后可以进行更新.增量(increment): 一种更新操作, 增加变量的值(常常是加1).减量(decrement): 一种更新操作, 减少变量的值.迭代(iteration): 使用递归函数调用或者循环来重复执行一组语句.无限循环(infinite loop): 一个终止条件永远无法满足的循环.算法(algorithm): 解决一类问题的通用过程.

7.9 练习

1. 练习1

复制7.5节的循环并封装到一个名为square_root的函数中, 这个函数接收一个形参a.
选择一个合理的值x, 并返回a的平方根的估计只.
要测试这个方法, 可以编写一个名称test_ssquare_root的函数 打印下面这样的表格:

a	  mysqrt(a)	      math.sqrt(a)	   diff
-     ---------       ------------     ----
1.0   1.000000000000  1.000000000000   0.0
2.0   1.414213562373  1.414213562373   2.220446049250313e-16
3.0   1.732050807569  1.732050807569   0.0
4.0   2.000000000000  2.000000000000   0.0
5.0   2.236067977500  2.236067977500   0.0
6.0   2.449489742783  2.449489742783   0.0
7.0   2.645751311065  2.645751311065   0.0
8.0   2.828427124746  2.828427124746   4.440892098500626e-16
9.0   3.000000000000  3.000000000000   0.0* 不要太纠结输出的格式, 有模有样就得了.

第一列是一个数, a; 
第二列是数a的平方根, 使用mysqrt函数计算.
第三列是使用math.sqrt计算出的平方根; 第四列是两种计算结果的差值的绝对值.

import mathdef square_root(a):x = 4while True:y = (x + a / x) / 2if x == y:breakx = yreturn ydef test_square_root(a):print('a	  mysqrt(a)	      math.sqrt(a)	   diff')print('-     ---------       ------------     ----')while a <= 9:square_1 = square_root(a)square_2 = math.sqrt(a)print(f'{a}  {square_1: .12f} {square_2: .12f}   {abs(square_1 - square_2)}')a = a + 1.0test_square_root(1.0)

2. 练习2

内置函数eval接收一个字符串并使用Python解释器对它进行求值. 例如:

>>> eval('1 + 2 + 3')
7>>> import math
>>> eval('math.sqrt(5)')
2.23606797749979>>> eval('type(math.pi)')
<class 'float'>

编写一个函数eval_loop, 迭代地提示用户, 接收它们的输入并使用eval求值, 并打印出结果.
它应当一直继续, 直到用户输入'done', 并返回最后一个求值的表达式的结果.

def eval_loop():# 初始化值.value = Nonewhile True:part = input('输入计算的表达式>:')if part == 'done':return valuevalue = eval(part)print(value)res = eval_loop()
print(res)

3. 练习3

数学家拉马努金(Srinivasa Ramanujan) 找到一个无限序列, 可以用来生成π的数值近似值:

编写一个函数estimate_pi, 使用这个公式计算并返回π的近似估计.
它应当使用一个while循环来计算求和的每一项, 
直到最后一项的值小于1e-15(这是Python对10-15(10的负15次方)的标记).
你可以通过和math.pi比较来检查计算的结果.
解答: https://github.com/AllenDowney/ThinkPython2/tree/master/code/pi.py

import mathdef factorial(n):"""递归计算n的阶乘."""if n == 0:return 1else:recurse = factorial(n - 1)result = n * recursereturn resultdef estimate_pi():"""计算π的估计值。Srinivasa Ramanujan的算法，来自http://en.wikipedia.org/wiki/Pi"""total = 0k = 0factor = 2 * math.sqrt(2) / 9801while True:num = factorial(4 * k) * (1103 + 26390 * k)den = factorial(k) ** 4 * 396 ** (4 * k)total += num / denterm = factor * num / denif abs(term) < 1e-15:breakk += 1return 1 / (factor * total)print(estimate_pi())