米哈游（原神）一面算法原题

小米汽车

近日，小米公布了财报。

小米 Q2 营收 889 亿，同比 +32%，调整后净利润 62 亿，同比 +20.1%。

营收符合预期，利润超预期 20 亿左右。

雷军说，这是小米成立以来最出色的财报。

有意思的是：小米汽车亏损 18 亿左右，结合销量来看，平均卖一台小米汽车，要亏损 6 万。

就这事儿还被极越的公关负责人在朋友圈指责：

不过很快这位当事人就公开道歉了。

明明亏这么多，为什么雷军还说这是出色财报？

因为据数据显示，小米汽车毛利率高达 15.4%，远超预期。

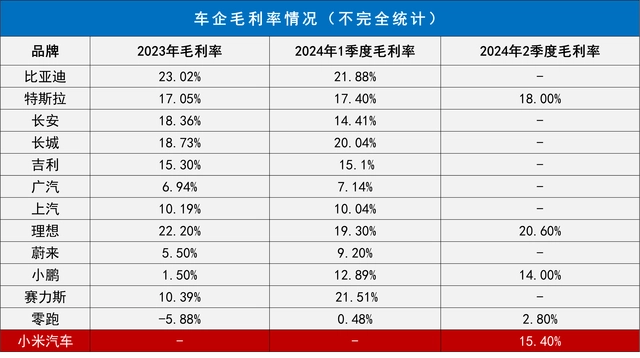
目前亏损只是因为小米汽车的前期投入（工厂建设、人员成本、研发支出等各项费用）尚未被销量摊开，将来如果产能上去，销量再上一个级别，利润由负转正的希望很大。

换句话说，如果将来小米汽车不亏钱，那么小米将会是一家年赚 300 亿的公司，如果小米汽车还能赚钱，那好家伙，你们自己想吧。

...

回归主线。

来一道和「米哈游（原神）」相关的算法题。

题目描述

平台：LeetCode

题号：646

给出 n 个数对。

在每一个数对中，第一个数字总是比第二个数字小。

现在，我们定义一种跟随关系，当且仅当 b < c 时，数对才可以跟在后面。我们用这种形式来构造一个数对链。

给定一个数对集合，找出能够形成的最长数对链的长度。你不需要用到所有的数对，你可以以任何顺序选择其中的一些数对来构造。

示例：

输入：[[1,2], [2,3], [3,4]]

输出：2

解释：最长的数对链是 [1,2] -> [3,4]

提示：

给出数对的个数在范围内。

排序 + 贪心 DP

起始先将 pairs 根据第一维排升序（或直接双关键字排升序）。

考虑定义为以为结尾的最长数对链长度，所有中的最大值为答案。

不失一般性考虑该如何转移：不难发现为所有满足「下标范围在，且」条件的的最大值。

但实际上，我们只需要从 j=i-1 开始往回找，找到第一个满足的位置 j 即可。

容易证明该做法的正确性：「假设贪心解（该做法）找到的位置不是最优位置，即存在比更小的合法下标满足。根据我们的排序规则必然有的性质，则可知必然可以代替接在原本以为结尾的最优数链上（最优数链长度不变，结果不会变差），则至少有。」

Java 代码：

class Solution {
    public int findLongestChain(int[][] pairs) {
        Arrays.sort(pairs, (a,b)->a[0]-b[0]);
        int n = pairs.length, ans = 1;
        int[] f = new int[n];
        for (int i = 0; i < n; i++) {
            f[i] = 1;
            for (int j = i - 1; j >= 0 && f[i] == 1; j--) {
                if (pairs[j][1] < pairs[i][0]) f[i] = f[j] + 1;
            }
            ans = Math.max(ans, f[i]);
        }
        return ans;
    }
}

C++ 代码：

class Solution {
public:
    int findLongestChain(vector<vector<int>>& pairs) {
        sort(pairs.begin(), pairs.end());
        int n = pairs.size(), ans = 1;
        vector<int> f(n, 1);
        for (int i = 0; i < n; i++) {
            f[i] = 1;
            for (int j = i - 1; j >= 0 && f[i] == 1; j--) {
                if (pairs[j][1] < pairs[i][0]) f[i] = f[j] + 1;
            }
            ans = max(ans, f[i]);
        }
        return ans;
    }
};

Python 代码：

class Solution:
    def findLongestChain(self, pairs: List[List[int]]) -> int:
        pairs.sort()
        n, ans = len(pairs), 1
        f = [1] * n
        for i in range(n):
            j = i - 1
            while j >= 0 and f[i] == 1:
                if pairs[j][1] < pairs[i][0]:
                    f[i] = f[j] + 1
                j -= 1
            ans = max(ans, f[i])
        return ans

TypeScript 代码：

function findLongestChain(pairs: number[][]): number {
    pairs.sort((a, b) => a[0] - b[0]);
    let n = pairs.length, ans = 1;
    const f: number[] = new Array(n).fill(1);    
    for (let i = 0; i < n; i++) {
        f[i] = 1;
        for (let j = i - 1; j >= 0 && f[i] == 1; j--) {
            if (pairs[j][1] < pairs[i][0]) f[i] = f[j] + 1;
        }
        ans = Math.max(ans, f[i]);
    }
    return ans;
};

时间复杂度：排序的复杂度为；不考虑剪枝效果 DP 复杂度为。整体复杂度为
空间复杂度：

排序 + 贪心 DP（优化转移）

根据上述分析，我们知道对于一个特定的而言，其所有合法（满足条件）的前驱状态必然是非单调递增的。

根据 LIS 问题的贪心解的思路，我们可以额外使用一个数组记录下特定长度数链的最小结尾值，从而实现二分找前驱状态。

具体的，创建 g 数组，其中代表数链长度为 len 时结尾元素的第二维最小值为 x。

如此一来，当我们要找的前驱状态时，等价于在 g 数组中找满足「小于」的最大下标。同时，我们不再需要显式维护 f 数组，只需要边转移变更新答案即可。

❝
「不了解 LIS 问题的同学可以看前置 🧀 : LCS 问题与 LIS 问题的相互关系，以及 LIS 问题的最优解证明 🎉🎉🎉」
❞

Java 代码：

class Solution {
    public int findLongestChain(int[][] pairs) {
        Arrays.sort(pairs, (a,b)->a[0]-b[0]);
        int n = pairs.length, ans = 1;
        int[] g = new int[n + 10];
        Arrays.fill(g, 0x3f3f3f3f);
        for (int i = 0; i < n; i++) {
            int l = 1, r = i + 1;
            while (l < r) {
                int mid = l + r >> 1;
                if (g[mid] >= pairs[i][0]) r = mid;
                else l = mid + 1;
            }
            g[r] = Math.min(g[r], pairs[i][1]);
            ans = Math.max(ans, r);
        }
        return ans;
    }
}

C++ 代码：

class Solution {
public:
    int findLongestChain(vector<vector<int>>& pairs) {
        sort(pairs.begin(), pairs.end());
        int n = pairs.size(), ans = 1;
        vector<int> g(n + 10, 0x3f3f3f3f);
        for (int i = 0; i < n; i++) {
            int l = 1, r = i + 1;
            while (l < r) {
                int mid = l + r >> 1;
                if (g[mid] >= pairs[i][0]) r = mid;
                else l = mid + 1;
            }
            g[r] = min(g[r], pairs[i][1]);
            ans = max(ans, r);
        }
        return ans;
    }
};

Python 代码：

class Solution:
    def findLongestChain(self, pairs: List[List[int]]) -> int:
        pairs.sort()
        n, ans = len(pairs), 1
        g = [0x3f3f3f3f] * (n + 10)
        for i in range(n):
            l, r = 1, i + 1
            while l < r:
                mid = l + r >> 1
                if g[mid] >= pairs[i][0]:
                    r = mid
                else:
                    l = mid + 1
            g[r] = min(g[r], pairs[i][1])
            ans = max(ans, r)
        return ans

TypeScript 代码：

function findLongestChain(pairs: number[][]): number {
    pairs.sort((a, b) => a[0] - b[0]);
    let n = pairs.length, ans = 1;
    const g: number[] = new Array(n + 10).fill(0x3f3f3f3f);
    for (let i = 0; i < n; i++) {
        let l = 1, r = i + 1;
        while (l < r) {
            const mid = l + r >> 1;
            if (g[mid] >= pairs[i][0]) r = mid;    
            else l = mid + 1; 
        }
        g[r] = Math.min(g[r], pairs[i][1]);
        ans = Math.max(ans, r);
    }
    return ans;
};