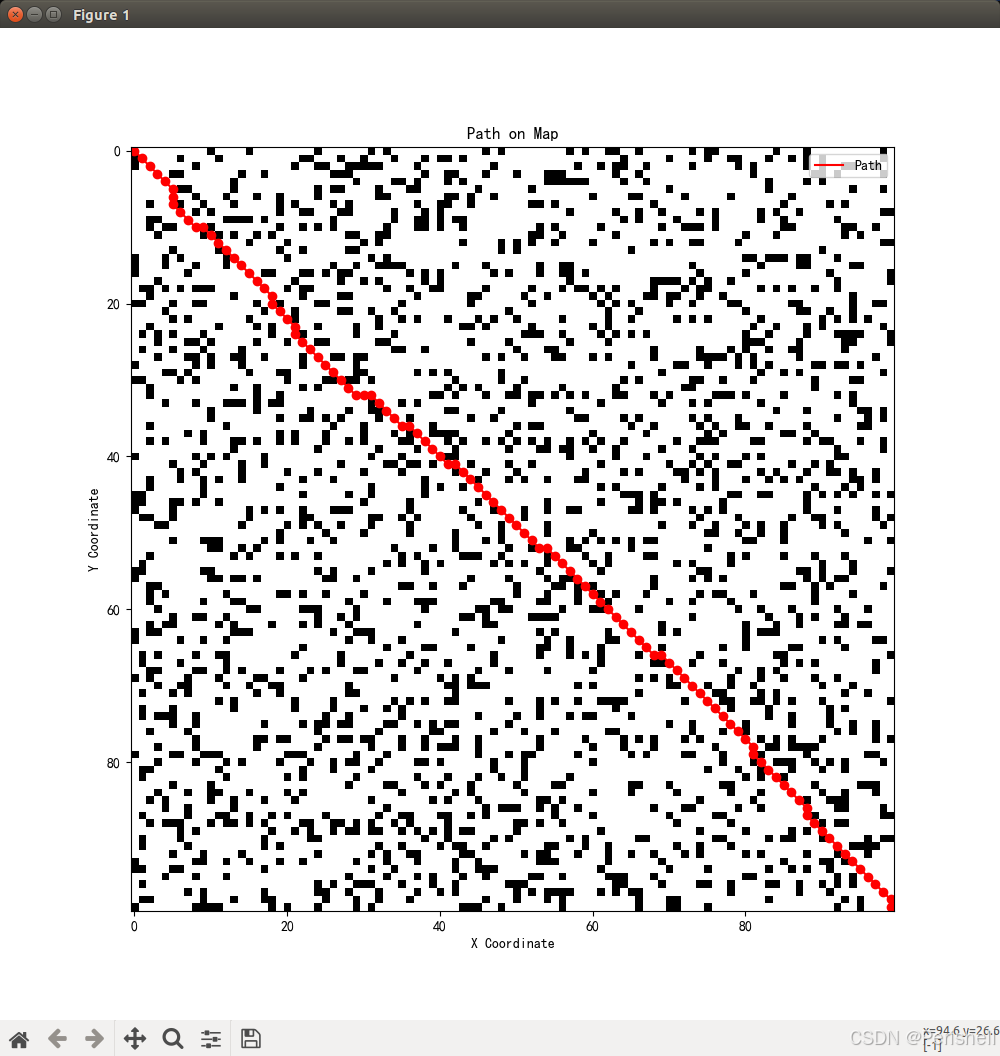
原来是用栅格地图的方式,0表示可通行区域,1表示不可通行区域,然后采用JPS算法做路径规划,从起点到终点规划出一条路径。但是目前我需要做的是将栅格地图更换为ESDF地图,那么JPS算法计算代价的部分是否需要进行变化。
栅格地图和ESDF地图的区别


首先,ESDF(Euclidean Signed Distance Field)地图不仅提供障碍物信息,还能给出每个点到最近障碍物的距离,这比二值化的栅格地图(0和1)包含更多信息。传统JPS在栅格中使用的是曼哈顿或欧氏距离作为启发式,而代价通常只是移动成本,比如每个格子的固定成本或者考虑地形因素。
JPS算法中代价函数修改策略
接下来需要考虑如何修改JPS的代价函数。传统JPS的g(n)是起点到当前节点的实际代价,h(n)是当前节点到终点的估计代价。在ESDF中,g(n)可能需要包括当前节点的ESDF值,比如用1/(d+1)或者指数衰减函数来增加靠近障碍物的节点的代价。同时,启发式函数h(n)可能仍然保持欧氏距离,但需要确保它是可接受的,即不会高估实际代价,否则A*可能找不到最优路径。
另外,节点之间的移动成本也需要调整。在栅格中,相邻节点移动成本通常是固定的,比如1。但在ESDF中,可能需要根据相邻节点的ESDF值来调整移动成本。例如,从高ESDF值(远离障碍物)移动到低ESDF值(靠近障碍物)的区域,成本会增加,从而避免路径靠近障碍物。
还需要考虑的是,ESDF地图中的距离值可能很大,直接使用这些值可能导致代价函数失衡,需要进行归一化或适当的缩放。例如,使用sigmoid函数将ESDF值转换为0到1之间的权重,再与其他因素结合。
可能的深层需求是希望路径在安全性和长度之间取得平衡。因此,代价函数可能需要一个权重参数,用来调整安全性和路径长度的优先级。比如,cost = distance_cost + safety_weight * safety_cost,这样用户可以通过调整safety_weight来改变路径的倾向。
另外,需要注意ESDF地图的计算是否正确,确保每个节点的距离值准确。如果ESDF地图中存在噪声或错误,可能会影响路径规划的结果。因此,预处理ESDF地图,比如平滑处理或去除小的错误区域,可能也是必要的。
ESDF地图特性与代价函数设计
def get_g(self, pos1, pos2):# ESDF安全代价(离障碍物越近代价越高)safety_weight = 0.6 # 安全系数(可调参数)slope_weight = 0.3 # 坡度权重(可调参数)d = self.ESDF_map[round(pos2[0])][round(pos2[1])]safety_cost = 1 / (abs(d) + 1e-5) # 距离越近代价越高# 坡度惩罚(可选)slope_penalty = abs(self.ESDF_map[round(pos1[0])][round(pos1[1])] - d)if pos1[0] == pos2[0]:return abs(pos1[1] - pos2[1]) + safety_weight * safety_cost + slope_penalty * slope_weightelif pos1[1] == pos2[1]:return abs(pos1[0] - pos2[0]) + safety_weight * safety_cost + slope_penalty * slope_weightelse:return abs(pos1[0] - pos2[0]) * 1.4 + safety_weight * safety_cost + slope_penalty * slope_weight启发函数改进
def heuristic(node, goal, esdf_map):# 基础欧式距离dx = abs(node.x - goal.x)dy = abs(node.y - goal.y)base_h = math.sqrt(dx**2 + dy**2)# 安全加成(可选)d = esdf_map[node.x][node.y]safety_h = 1 / (d + 1) # 离障碍物越近启发值越高return base_h + 0.3 * safety_h # 加权组合关键参数说明
| 参数 | 推荐值 | 作用 |
|---|---|---|
safety_weight | 0.3-0.8 | 安全避障权重 |
slope_penalty | 0.1-0.3 | 地形起伏惩罚 |
| 安全距离阈值 | 3-5 cells | 拒绝进入该距离内的区域 |
效果对比
| 指标 | 原始A* | ESDF-A* |
|---|---|---|
| 路径长度 | 最短 | 略长1-5% |
| 安全距离 | 可能贴障碍物 | 保持安全距离 |
| 计算时间 | 快 | 增加20-40% |
| 适用场景 | 简单环境 | 动态/复杂环境 |
仿真结果