(Ⅰ)神经网络和深度学习
一,ReLU激活函数
ReLU(Rectified Linear Unit)函数,输入大于0时,直接输出该值;输入小于0时,输出0

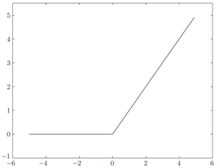
代码实现:


图中的每个节点都可以是ReLU激活函数的一部分
二,循环神经网络(Recurrent Neural Network,RNN)
RNN,神经网络的一种,对具有序列特性的数据非常有效,能挖掘数据中的时序信息以及语义信息。(序列特性:符合时间顺序,逻辑顺序等其他顺序的性质)
结构:

循环神经网络中,上一次的输出将会作为下一次的输入
三,计算图
计算图的导数计算-链式求导:
计算图中的反向传播将局部导数从右往左传播,基于链式求导法则

将信号E乘以节点的局部导数,然后传递给下一节点(如上图)
链式求导法则则是基于复合函数求导,描述局部值的变化对输出值的影响

四,numpy
(1)利用numpy中的np.dot()实现向量化计算
时间复杂度和for循环方法均为O(n),但是实际执行时间比for循环快100-1000倍
原因:
①np.dot()可以减少python解释器循环的开销:np.dot()可以不用检查下标i是否越界,解析a[i] b[i]的数据类型,可以减少时间
②np.dot()可以实现SIMD指令优化
③np.dot()可以实现CPU缓存预取:可以准确访问每个值,提前加载,进行计算
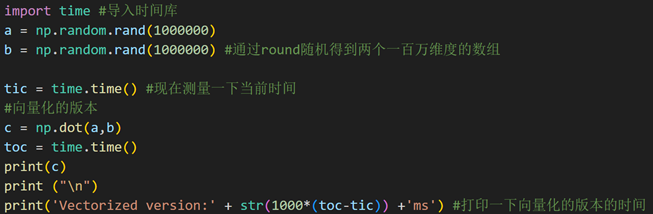

(2)numpy向量化实现逻辑回归

(3)numpy的广播机制:
numpy的广播机制是一种高效处理不同形状数组间的运算规则,允许逐个元素操作而无需复制

Example1:
利用np.sum(axis=0)实现矩阵按列求和
np.sum(axis=1)实现矩阵按行求和

Example2:
numpy面对不同形状的矩阵时,允许逐个元素进行相应的计算操作

等价于

Example3:

等价于

(4)numpy中向量的说明:
当用调用np.array()创建数组时,不推荐创建秩为1的简单数组,而是直接创建成列向量or行向量

直接创建秩为1的数组时,容易产生bug
五,激活函数
(1)tanh激活函数:
tanh激活函数是sigmoid平移伸缩的结果,拟合效果在所有场合都优于sigmoid,且几乎适用于所有场合。
(二分类输出层使用sigmoid是因为想让输出结果介于[0,1],所以使用sigmoid)

(2)LeakyReLU激活函数:
ReLU的改良版,当输入为负值时,输出值不为0,而是稍微倾斜,激活效果比ReLu好

(3)激活函数的选择
①二分类问题,输出层选择sigmoid,其他所有单元选择ReLU
②在实践中,ReLU的学习速度快于sigmoid,因为sigmoid要进行浮点四则运算
③隐藏层通常选择ReLU,也会选择tanh(注:选择ReLU时,输入为负值时,输出0)
④不能在隐藏层使用线性激活函数,唯一可以使用线性激活函数的通常是输出层:因为线性激活函数导数通常是常数,梯度下降时梯度值不变
六,随机初始化
对于一个神经网络,初始化权重(W)和其他参数为0时,无法进行梯度下降,并且由于对称性,反向传播的导数也是一样的,激活函数也是一样的。无论花多少时间拟合,都是一样的,拟合效果差(对于逻辑回归,可以初始化权重为0)

可以随机初始化权重(W),初始化为一个很小很小的数(通常为0.01),若一开始初始化为很大很大的数,激活函数(sigmoid/tanh)的函数值就会趋向平稳,学习速率慢
七,深层神经网络

深层神经网络本质上就是更复杂的,包含更多隐藏层的神经网络(如上图)
(1)符号表示
L:表示神经网络的层数(隐藏层+输出层)
n[x]:表示第x层的神经网络有n[x]个神经元
a[x]:表示第x层的神经网络的激活函数
W[x]:表示第x层的权重
此外,输入层为a[0],输出层(y-hat)为a[L]
(2)深层神经网络的向前传播和反向传播
本质上和普通神经网络的向前传播和反向传播无异,只是计算较为复杂
向前传播(向量化):

反向传播:

(3)核对神经网络中矩阵的维数:
根据已知数据(输入层,输出层,激活函数等),通过已知数据的矩阵的维度,依据矩阵乘法法则,来倒推权重(W),和偏置(b)的维度,以此来检验神经网络中矩阵的维数。

(4)深层神经网络的优点:
深层神经网络较普通神经网络,隐藏层的数目更多,可以提取到的特征的复杂度更大;且深层神经网络可以减少神经元的个数,减少计算量,从而加快学习速率
深层神经网络应用于图像处理中,可以提取更丰富的特征,由简单到复杂,越复杂,准确率就越高
(5)神经网络块表示深层神经网络(类似计算图):
可以表示正向传播和反向传播,类似于计算图

(6)参数和超参数:
参数:权重(W),偏置(b),是模型在训练过程中自动学习的变量,用于拟合数据和做出预测,数量级非常大(百万级)
超参数:隐藏层数(L),学习率,迭代次数,是模型在训练前手动设置的,不通过数据学习,控制训练过程,数量级通常较少
两者形成合适的组合可以实现模型的最优:参数实现具体拟合,超参数实现模型的潜力
(Ⅱ)深层神经网络的优化
一,数据集(训练集+验证集+测试集)
训练集:拟合模型
验证集:调整模型超参数和初步评估模型能力
测试集:最终评估模型
数据集的切分:
小数据时代:通常是验证:测试=7:3 或者 训练:验证:测试=6:2:2
大数据时代:训练集的比例通常占据大部分,占据99%以上,验证集和测试集比例减少
数据集的来源最好保证统一,可以使得模型泛化能力更好
二,偏差-方差困境
偏差-方差困境是模型复杂度和泛化能力之间的根本矛盾,核心目标是找到偏差和方差的平衡点,使得模型总误差最小

偏差和方差在模型中的应用:

三,正则化
L1正则化 和 L2正则化
(1)L1正则化:

L1正则化倾向于将部分参数压缩到0,从而实现特征选择,自动筛选重要特征,适用于特征维度较高,且需要减少特征数量的场景。
但是对异常值敏感,当特征高度相关时,可能随机选择一个特征,忽略其他特征
(2)L2正则化:

L2正则化更倾向于让所有参数接近0但不为0,保持参数平滑分布,使用于特征之间高度相关
(3)为什么正则化可以减少过拟合:
核心原理是正则化通过在模型训练过程中加入额外的约束(即正则化参数项用来惩罚),从而限制模型参数的复杂度,从而防止过拟合
以逻辑回归为例:

当正则化参数(λ)初始值很大时,权重(W)会接近于0,使得神经网络中的神经元作用变得很小,整个神经网络更接近逻辑回归。
(4)dropout正则化:
Dropout正则化通过随机”丢弃”神经元来防止模型过拟合,适用于深度神经网络
实施步骤:
遍历神经网络的每一层 ---> 随机为神经网络中的每个节点设置消除的概率 ---> 删除节点后,移除所有从该节点进入和出去的连接 ---> 最终得到较小的神经网络 ---> 反向传播
dropout实现方法(Inverted Dropout):
Inverted Dropout在训练阶段对保留的神经元进行缩放,缩放激活值,从而使得训练和测试阶段的激活值期望一致,从而无需在测试时调整参数
(训练和测试阶段激活值期望一致,可以避免预测偏差,确保模型输出在训练和测试时候的分布一致;且使得梯度稳定,权重正确收敛)
dropout的功能类似于L2正则化,对于不同的神经网络层,使用不同的消除概率(对于参数集中的层,使用较低的消除概率)。但是dropout需要交叉验证更多的参数(由于dropout中损失函数不再被明确定义,每次迭代,都会随机移除一些节点,很难复查梯度下降的性能。在实际操作中,可以先关闭dropout,确保损失函数单调递减,然后在开启dropout)
(5)其他正则化方法:
①数据扩增:用于处理图片数据(扩增数据集通常成本较高),可以通过水平翻转,随意裁剪,旋转,放大等扩增数据,进而正则化数据集,减少过拟合
对于数字识别,可以对数字进行扭曲,旋转

②Early stopping:
Early stopping,提前停止。
在模型训练过程中监控验证集性能,及时终止训练以防止过拟合。
在模型开始过拟合之前停止训练,从而在偏差和方差之间取得平衡(即在验证集误差和训练集误差同时取得最低点时终止训练)

Early stopping可以只进行一次梯度下降,找出权重(W)的较小值,中间值和最大值,与L2正则化相比,无需尝试更多正则化参数,且比L2正则化训练时间少,成本低
但是Early stopping不能同时处理过拟合和损失函数不够小的问题。
四,输入归一化
(1)输入归一化,一种数据预处理的技术。可以加速模型训练
实现步骤:
①减去或归零均值:将数据集中的所有数据减去均值
②归一化方差:将所有数据除以方差

实现目的:”优化”损失函数,使损失函数的图像更”圆润”。可以使用较大的学习率,更快的找到最优的权重(W)和偏置(b)

(2)梯度消失与梯度爆炸:
梯度消失:反向传播时,梯度随着网络深度逐层减少,最终接近于0,使得浅层参数几乎不更新。导致模型训练停滞,损失函数无法下降。
梯度爆炸:梯度随着网络深度指数级增长,数值超出范围。导致模型参数更新步长过大,模型发散

解决方法:
神经网络权重初始化:

为了防止Z的值过大或过小(Z=W·X),当输入特征数量n越大时,权重(W)越小。
可以设置权重(W)的方差=1/n来实现。
在实践中可以设置网络中某层的权重矩阵为


(3)梯度检验:
梯度数值的逼近:在反向传播时,计算误差,需要使用双边误差而不使用单边误差来逼近梯度的数值

梯度检验:用来验证神经网络中反向传播梯度计算的正确性。通过上述方法计算近似梯度,与解析梯度对比,来确保代码的无误。

实现步骤:
①参数向量化:将神经网络中的所有参数(权重W,偏置b)拼接成一个一维向量θ
②中心差分法进行梯度计算:对于每个θ加以轻微扰动(1e-5 - 1e-7),计算损失函数变化量,近似梯度

③将理论值的梯度和近似值的梯度对比,进行检查。
(4)Mini-batch梯度下降:
Mini-batch梯度下降适用于处理巨大的数据集。
面对巨大的数据集,向量化虽然可以加速梯度下降,但是进行下一次梯度下降时,必须完成当前次的梯度下降,导致速率低下
Mini-batch梯度下降,将巨大的数据集分割成较小的子集(即Mini-batch),每次只用处理单个较小的训练子集,从而实现梯度的下降

Batch梯度下降 VS Mini-batch 梯度下降
由于Mini-batch梯度下降时的学习率过大,且每次迭代都在训练不同的数据子集,会导致Mini-batch的损失函数跌宕起伏,但是总体上呈下降趋势
Mini-batch梯度下降中Mini-batch size的选择:
Size=m,即等于数据集大小,就是batch梯度下降,速率慢
Size=1,随机梯度下降法,梯度下降波动较大,不稳定
Size在(1,m)Mini-batch一般选择64,128等2的幂次

五,指数加权平均数

指数加权平均数通过对历史数据赋予指数衰减的权重来计算移动平均值
越近期的数据对当前平均值的影响越大,而历史数据的影响随指数衰减

上图中:
红β=0.9,表示过去10天的平均气温
绿β=0.98,表示过去50天的平均气温,曲线平缓
黄β=0.5,表示过去2天的平均气温,曲线抖动明显,适应快
六,动量梯度下降法
计算梯度的指数加权平均数,然后使用该梯度更新权重(W)

上图为标准的梯度下降,中心红点为最小的权重(W)和偏置(b)。标准的梯度下降会上下波动,且要使用较小的学习率,否则会偏离(如紫线)
使用动量梯度下降法:
可以引入动量项,将历史的梯度方向积累到当前更新中。可以在梯度方向一致的维度加速更新,减少震荡。(注:动量梯度下降法适用于碗状)

七,RMSprop
Root Mean Square Propagation,自适应学习率的优化算法。可以动态调整每个参数的学习率,提升模型的训练效率和稳定性

更新步骤:
①计算梯度平方的指数加权平均数

②更新参数:

RMSprop和动量梯度下降法类似,可以消除梯度下降和Mini-batch梯度下降的摆动,并且可以使用一个较大的学习率,加快学习速率
八,Adam算法
Adam算法=动量梯度下降+RMSprop
可以动态调整每个参数的学习率,同时利用梯度的均值和方差来实现更新
实现步骤:
①计算均值
②计算方差
③偏差矫正
④参数更新
九,学习率衰减

梯度下降时,若使用固定的学习率(如蓝线),则可能会找不到最低点;使用衰减的学习率,在学习初期,使用较大的学习率,可以加快学习速度。开始收敛的时候,使用较小的学习率,缓慢靠近最低点。
梯度下降中,面对局部最优:

高纬度空间中,极低的概率会遇到左图所示的局部最优点,大部分情况可能是如右图所示的鞍点
且基本上不会遇见局部最优问题,常见的可能是平稳段(如下图),减缓了学习速率,该梯度接近于0。可以利用上述方法加速。





