相控阵天线——基于MATLAB对线阵进行泰勒加权
目录
前言
一、泰勒综合
二、单元间距的改变对泰勒阵列方向图的影响
三、单元数的改变对泰勒阵列激励分布的影响
四、副瓣电平SLL对泰勒阵列激励幅度的影响
五、副瓣电平SLL对泰勒阵列方向图的影响
六、泰勒阵列和切比雪夫阵列的比较
七、副瓣电平和阵元个数间的关系
八、MATLAB代码
总结
前言
前面讨论了经典的道尔夫-切比雪夫综合方法,由此得到的切比雪夫阵列其方向图是最佳的,即在相同阵列长度情况下对给定的副瓣电平,其主瓣宽度是最窄的,或对给定的主瓣宽度,所得副瓣电平是最低的。但切比雪夫阵列两端单元的激励幅度容易发生跳变,不利于馈电。与切比雪夫综合法密切相关的另外一种经典综合方法一一泰勒综合法。采用泰勒综合法设计的泰勒阵列,其方向图只是靠近主瓣某个区域内的副瓣电平接近相等,随后单调地减小。如果设计得当,激励幅度分布的变化在阵列两端是单调减的,不会出现两端单元激励幅度跳变的情况。本文介绍根据方向图的副瓣电平对相控阵线阵天线进行泰勒加权(综合),并通过MATLAB仿真分析泰勒加权方法的优缺点。
提示:以下是本篇文章正文内容,欢迎各位阅读,转载请附上链接。
一、泰勒综合
采用泰勒综合法设计的泰勒阵列,其方向图只是靠近主瓣某个区域内的副瓣电平接近相等,随后单调地减小,有利于提高天线方向性系数。如果设计得当,激励幅度分布的变化在阵列两端是单调减的,不会出现两端单元激励幅度跳变的情况。泰勒综合法设计灵活,适应面宽,在工程设计中得到广泛应用。
对于一个长为L的连续线源,其空间因子(即方向图函数)可表示为:
此式即为理想的空间因子。根据u的取值可分为主瓣区和副瓣区:
,为主瓣区:
,为副瓣区:
引入基本函数
引入波瓣展宽因子,改造理想空间因子:
其零点位置为:
改造基本函数构建泰勒空间因子:
该空间因子的含义是:把基本函数的前元个零点用改造的理想空间因子的零点取代,而第
个以 后的零点保持为基本函数的零点,即
典型的问题是对单元数为N,间距为d的直线阵,采用泰勒综合法综合其激励分布(各单元的激励电流I),使其阵因子方向图的副瓣电平为 dB。
显然,秦勒综合时的已知参数是N、d和。泰勒综合步骤如下:
① 计算,其中int表示取整数部分
② 确定单元位置
这样确定的单元位置对奇、偶数阵列均可,但所得I是从左到右顺序排列的。
③ 确定变量
④ 计算各单元的激励电流
其中
对于泰勒加权可以直接通过以上步骤去综合,也可以直接使用MATLAB自带的函数去综合。这里我们使用MATLAB自带的函数去综合。
I=taylorwin(N,n_bar,SLL); %N为阵元数,n_bar是公式中的符号,SLL为副瓣电平,I包含各阵元的激励幅度
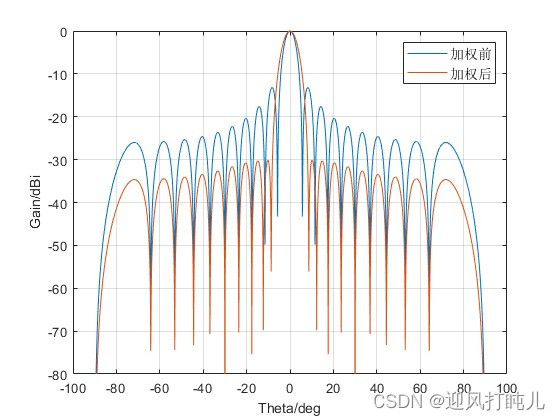
仿真参数设置为:
f=2e9; %频率,单位Hz
N=20; %阵元数
mu=1/2; %阵元间距÷波长
theta0=0;%波束指向角度,单位°
SLL=-30; %副瓣电平,单位dB
二、单元间距的改变对泰勒阵列方向图的影响
仿真参数设置如下:
f=2e9; %频率,单位Hz
N=10; %阵元数
theta0=0;%波束指向角度,单位°
SLL=-20; %副瓣电平,单位dB
依次设置,
,
,
,观察方向图及激励幅度分布。


可知,随着间距的增大,主瓣宽度变窄,副瓣增多,当时方向图出现栅瓣。
三、单元数的改变对泰勒阵列激励分布的影响
仿真参数设置如下:
f=2e9; %频率,单位Hz
theta0=0;%波束指向角度,单位°
mu=1/2; %阵元间距÷波长
当SLL=-20dB时,依次设置N=15,20,25,30,35,观察激励幅度的分布;当SLL=-40dB时,依次设置N=15,20,25,30,35,观察激励幅度的分布。
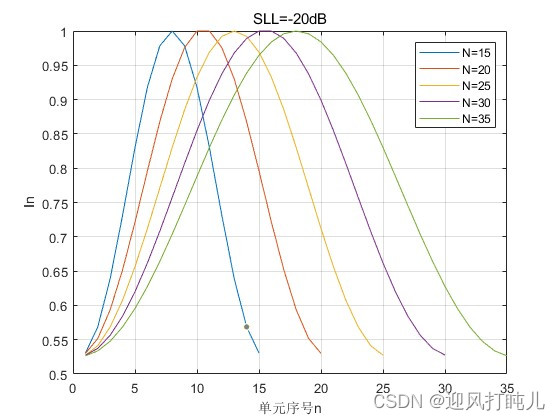
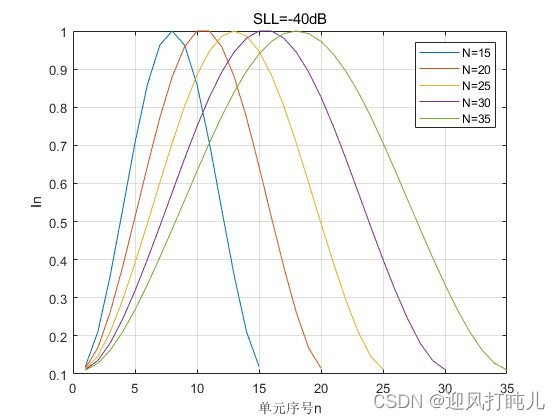
可见,泰勒阵列两端单元的激励幅度不会像切比雪夫阵列那样发生跳变。
四、副瓣电平SLL对泰勒阵列激励幅度的影响
仿真参数设置如下:
f=2e9; %频率,单位Hz
theta0=0;%波束指向角度,单位°
mu=1/2; %阵元间距÷波长
N=20; %阵元数
当N=20时,依次设置SLL=-20,-25,-30,-35,-40dB,观察激励幅度的分布。
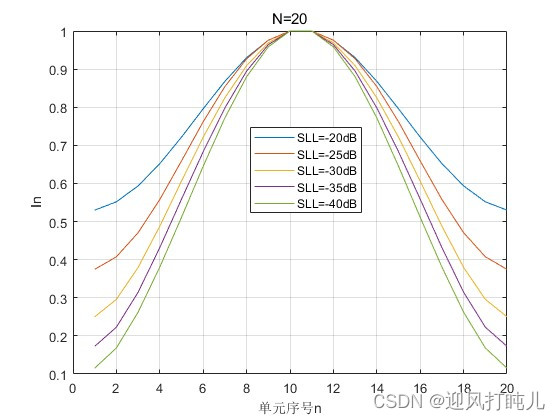
五、副瓣电平SLL对泰勒阵列方向图的影响
仿真参数设置如下:
f=2e9; %频率,单位Hz
N=16; %阵元数
theta0=20;%波束指向角度,单位°
mu=1/2; %阵元间距÷波长
依次设置SLL=-10,-20,-30,-40dB,观察方向图。
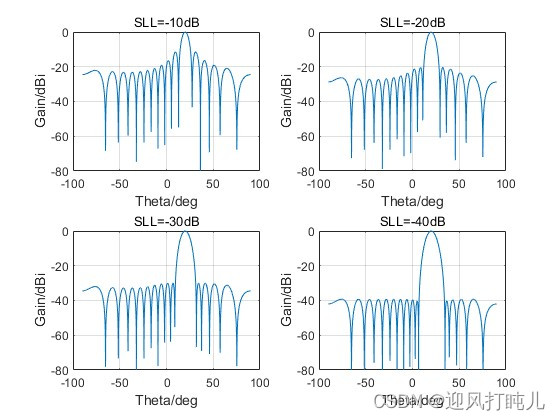
由图可见,单元数N和间距d不变,随着方向图副瓣电平的降低,主瓣宽度将略有增大。当副瓣电平比较低时,泰勒阵列和切比雪夫阵列的方向图比较接近。
六、泰勒阵列和切比雪夫阵列的比较
仿真参数设置如下:
f=2e9; %频率,单位Hz
N=32; %阵元数
theta0=0;%波束指向角度,单位°
mu=1/2; %阵元间距÷波长
SLL=-30; %副瓣电平,单位dB


可见,切比雪夫综合得到的激励幅度分布在阵列两端出现了跳变,而泰勒综合方法所得结果则为单调减少的。切比雪夫综合方法得到的方向图为等副瓣电平,而泰勒综合方法得到的方向图副瓣电平只有紧靠主瓣的几个副瓣电平接近相等,其余副瓣电平是递减的。
在相同单元数和单元间距的情况下,泰勒阵列的副瓣越低,则其激励分布和方向图就越接近相同情况下的切比雪夫阵列。
七、副瓣电平和阵元个数间的关系
一个N单元阵列,当d=时,其方向图的零点个数为N-1,主瓣两侧各有副瓣N/2-1个,应有
,则
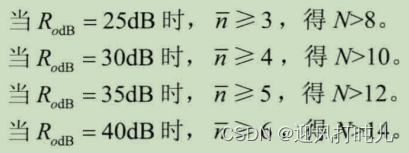
八、MATLAB代码
https://download.csdn.net/download/m0_66360845/89493202![]() https://download.csdn.net/download/m0_66360845/89493202
https://download.csdn.net/download/m0_66360845/89493202
总结
以上就是今天要分享的全部内容,本文介绍了泰勒加权方法对线阵进行综合,同时也分析了间距、单元数,副瓣电平等参数对激励幅度以及方向图的影响,最后还比较了切比雪夫加权和泰勒加权。






