1161. 最大层内元素和 - 力扣(LeetCode)
题目
给你一个二叉树的根节点 root。设根节点位于二叉树的第 1 层,而根节点的子节点位于第 2 层,依此类推。
请返回层内元素之和 最大 的那几层(可能只有一层)的层号,并返回其中 最小 的那个。
示例 1:
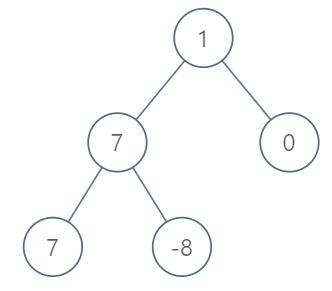
输入:root = [1,7,0,7,-8,null,null] 输出:2 解释: 第 1 层各元素之和为 1, 第 2 层各元素之和为 7 + 0 = 7, 第 3 层各元素之和为 7 + -8 = -1, 所以我们返回第 2 层的层号,它的层内元素之和最大。
示例 2:
输入:root = [989,null,10250,98693,-89388,null,null,null,-32127] 输出:2
提示:
- 树中的节点数在
[1, 104]范围内 -105 <= Node.val <= 105
思路
- 仍是采用广度优先搜索,逐层统计各层的元素和,但是过程中需记录深度。
- 一开始记录root->val为最大和,往下统计当且仅当当前层大于最大和时更新最大和的值和最大和的深度。
- 统计完所有层后返回最大和的深度即可。
代码实现
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:int maxLevelSum(TreeNode* root) {queue<TreeNode*> layer1, layer2;int depth = 1, sum = 0, max_depth = 1, maxn;TreeNode* node;layer1.push(root);maxn = root->val;bool flag = true;while(!layer1.empty() || !layer2.empty()) {if(flag) {node = layer1.front();sum += node->val;if(node->left) layer2.push(node->left);if(node->right) layer2.push(node->right);layer1.pop();if(layer1.empty()) {if(maxn < sum) {maxn = sum;max_depth = depth;}flag = !flag;sum = 0;depth++;}}else {node = layer2.front();sum += node->val;if(node->left) layer1.push(node->left);if(node->right) layer1.push(node->right);layer2.pop();if(layer2.empty()) {if(maxn < sum) {maxn = sum;max_depth = depth;}flag = !flag;sum = 0;depth++;}}}return max_depth;}
};复杂度分析
- 时间复杂度:每个元素仅涉及一次出入队,时间复杂度为O(n)。
- 空间复杂度:取决于元素最多的一层的元素数,最差空间复杂度近似于O(n)。



)

