算法日记14：SC339（二维联通，洪水灌溉）DFS+set

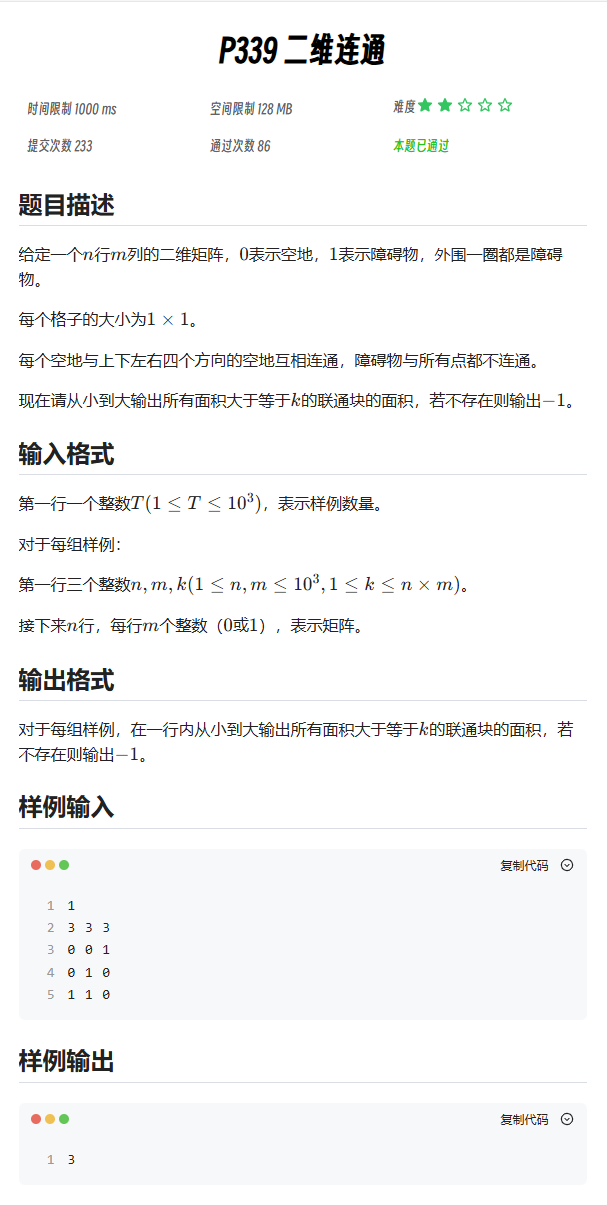
一、题目

二、题解：

2.1：由题目得出，此题为类迷宫问题，因此我们可以考虑DFS/BFS

• 假如使用DFS来解决问题，可以得出时间复杂度为$O(n\ast m)$，且$(1\le n,m\le 10^3)$，因此时间复杂度大致为$1e9$，可以解决问题
• BFS同理，一样为$1e9$

2.2:首先，让我们来用DFS来解决问题

1、因为题目要求我们按照升序来进行答案的输出，因此我们可以考虑使用$set()$函数/使用(vector+sort)

2、在迷宫问题中，我们需要考虑不能重复访问同一块区域的问题，因此我们使用st[N]数组来表示某个点是否范围过

const int N = 1007;
int g[N][N];
bool st[N][N];  //用来统计这个点是否被计算过
int n,m,k;
set<int>res;    //存储答案

3、样例的输入：应当是访问到合理的区局块时（如果[x][y]没有被走过,并且可以走），才开始计算面积，也就是才开始调用DFS函数来进行这个区域的覆盖+面积计算

for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){        if(st[i][j]==false && g[i][j]==0) //如果[x][y]没有被走过,并且可以走{int cnt=dfs(i,j);if(cnt>=k) res.insert(cnt);}       }}

• 这样，既防止了重复访问，又减轻的时间复杂度

4、DFS函数

• 1):因为我们需要计算一整块的面积总和（每一块洪水区域的方块总和）因此需要使用int型的DFS递归函数
• 2):在每一次DFS的递归过程中，我们一直往下递，直到访问到了非法的边界，就开始归(return) 一步步求出总的面积和，最后返回递归的总和即可

int dx[]={0,1,0,-1};
int dy[]={1,0,-1,0};
int dfs(int x,int y)    //能进DFS意味着一定可以走
{int temp=1; //用来存储单块面积st[x][y]=true;  //走for(int i=0;i<4;i++)    //四联通{int a=x+dx[i],b=y+dy[i];if(a<1 || a>n || b<1 || b>m) continue;  //越界if(st[a][b]==true) continue;    //走过不走if(g[a][b]==1) continue;    //表示障碍物,不走temp+=dfs(a,b); //面积+dfs块}return temp;
}

5、注意题目中有多个样例，因此在每一轮的样例中，都要清空状态数组st和答案数组set<int>res

//清空
res.clear();
memset(st,0,sizeof(st));

三、完整代码

#include<bits/stdc++.h>
using namespace std;const int N = 1007;
int g[N][N];
bool st[N][N];  //用来统计这个点是否被计算过
int n,m,k;
set<int>res;    //存储答案int dx[]={0,1,0,-1};
int dy[]={1,0,-1,0};int dfs(int x,int y)    //能进DFS意味着一定可以走
{int temp=1; //用来存储单块面积st[x][y]=true;  //走for(int i=0;i<4;i++)    //四联通{int a=x+dx[i],b=y+dy[i];if(a<1 || a>n || b<1 || b>m) continue;  //越界if(st[a][b]==true) continue;    //走过不走if(g[a][b]==1) continue;    //表示障碍物,不走temp+=dfs(a,b); //面积+dfs块}return temp;
}void solve() 
{//清空res.clear();memset(st,0,sizeof(st));cin>>n>>m>>k;for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){cin>>g[i][j];}}for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){        if(st[i][j]==false && g[i][j]==0) //如果[x][y]没有被走过,并且可以走{int cnt=dfs(i,j);if(cnt>=k) res.insert(cnt);}       }}if(res.empty()) //set为空{cout<<-1<<'\n';return ;}for(auto i:res){cout<<i<<' ';}
}int main() {ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);int _ = 1;cin>>_;while (_--) solve();return 0;
}