CONTENTS
- LeetCode 146. LRU 缓存(中等)
- LeetCode 147. 对链表进行插入排序(中等)
- LeetCode 148. 排序链表(中等)
- LeetCode 149. 直线上最多的点数(困难)
- LeetCode 150. 逆波兰表达式求值(中等)
LeetCode 146. LRU 缓存(中等)
【题目描述】
请你设计并实现一个满足 LRU(最近最少使用)缓存约束的数据结构。
实现 LRUCache 类:
LRUCache(int capacity)以正整数作为容量capacity初始化 LRU 缓存;int get(int key)如果关键字key存在于缓存中,则返回关键字的值,否则返回 -1。void put(int key, int value)如果关键字key已经存在,则变更其数据值value;如果不存在,则向缓存中插入该组key-value。如果插入操作导致关键字数量超过capacity,则应该逐出最久未使用的关键字。
函数 get 和 put 必须以 O ( 1 ) O(1) O(1) 的平均时间复杂度运行。
【示例 1】
输入
["LRUCache", "put", "put", "get", "put", "get", "put", "get", "get", "get"]
[[2], [1, 1], [2, 2], [1], [3, 3], [2], [4, 4], [1], [3], [4]]
输出
[null, null, null, 1, null, -1, null, -1, 3, 4]解释
LRUCache lRUCache = new LRUCache(2);
lRUCache.put(1, 1); // 缓存是 {1=1}
lRUCache.put(2, 2); // 缓存是 {1=1, 2=2}
lRUCache.get(1); // 返回 1
lRUCache.put(3, 3); // 该操作会使得关键字 2 作废,缓存是 {1=1, 3=3}
lRUCache.get(2); // 返回 -1 (未找到)
lRUCache.put(4, 4); // 该操作会使得关键字 1 作废,缓存是 {4=4, 3=3}
lRUCache.get(1); // 返回 -1 (未找到)
lRUCache.get(3); // 返回 3
lRUCache.get(4); // 返回 4
【提示】
1 < = c a p a c i t y < = 3000 1 <= capacity <= 3000 1<=capacity<=3000
0 < = k e y < = 10000 0 <= key <= 10000 0<=key<=10000
0 < = v a l u e < = 1 0 5 0 <= value <= 10^5 0<=value<=105
最多调用 2 ∗ 1 0 5 2 * 10^5 2∗105 次 get 和 put
【分析】
使用哈希表可以实现时间复杂度为 O ( 1 ) O(1) O(1) 的增删改查,但是还需要实现 LRU 的机制,我们要能够修改每个键值对的时间戳,同时还能够快速找到时间戳最小的键值对。
可以用一个双链表维护这个时间戳,时间戳最新的节点在头部,最旧的节点在尾部,哈希表用于从 key 映射到对应的节点,这样查找双链表的节点就是 O ( 1 ) O(1) O(1) 的,从而双链表的插入与删除操作也是 O ( 1 ) O(1) O(1) 的。
【代码】
class LRUCache {
private:struct Node {int key, val;Node *left, *right;Node(int key, int val): key(key), val(val), left(nullptr), right(nullptr) {}}*L, *R;int n;unordered_map<int, Node*> hash;void insert(Node* p) { // 将 p 插入到链表的首部p->left = L, p->right = L->right;L->right->left = p, L->right = p;}void remove(Node* p) { // 将 p 从链表中删除p->left->right = p->right;p->right->left = p->left;}public:LRUCache(int capacity) {n = capacity;L = new Node(-1, -1), R = new Node(-1, -1);L->right = R, R->left = L;}int get(int key) {if (!hash.count(key)) return -1;Node* p = hash[key];remove(p);insert(p);return p->val;}void put(int key, int value) {if (!hash.count(key)) {if (hash.size() == n) // 容量满了则删除链表的最后一个点hash.erase(R->left->key), remove(R->left);hash[key] = new Node(key, value);insert(hash[key]);} else {Node* p = hash[key];p->val = value;remove(p);insert(p);}}
};/*** Your LRUCache object will be instantiated and called as such:* LRUCache* obj = new LRUCache(capacity);* int param_1 = obj->get(key);* obj->put(key,value);*/
LeetCode 147. 对链表进行插入排序(中等)
【题目描述】
给定单个链表的头 head,使用插入排序对链表进行排序,并返回排序后链表的头。
插入排序算法的步骤:
- 插入排序是迭代的,每次只移动一个元素,直到所有元素可以形成一个有序的输出列表。
- 每次迭代中,插入排序只从输入数据中移除一个待排序的元素,找到它在序列中适当的位置,并将其插入。
- 重复直到所有输入数据插入完为止。
下面是插入排序算法的一个图形示例。部分排序的列表(黑色)最初只包含列表中的第一个元素。每次迭代时,从输入数据中删除一个元素(红色),并就地插入已排序的列表中。
对链表进行插入排序。
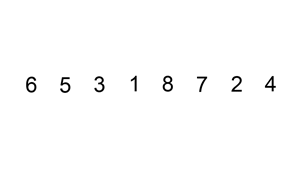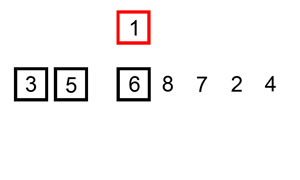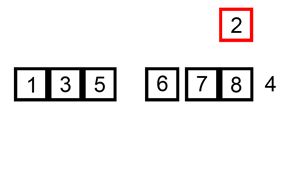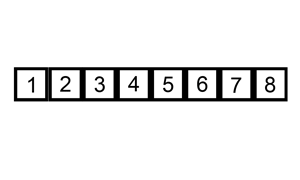
【示例 1】

输入: head = [4,2,1,3]
输出: [1,2,3,4]
【示例 2】

输入: head = [-1,5,3,4,0]
输出: [-1,0,3,4,5]
【提示】
列表中的节点数在 [ 1 , 5000 ] [1, 5000] [1,5000] 范围内
− 5000 < = N o d e . v a l < = 5000 -5000 <= Node.val <= 5000 −5000<=Node.val<=5000
【分析】
对于当前要插入的点,我们要在已排序区间中找到第一个大于当前点的位置,将当前点插入到这个更大的点的前面。如果当前点前面的点都小于等于自身,则直接插入在区间末尾即可。
【代码】
/*** Definition for singly-linked list.* struct ListNode {* int val;* ListNode *next;* ListNode() : val(0), next(nullptr) {}* ListNode(int x) : val(x), next(nullptr) {}* ListNode(int x, ListNode *next) : val(x), next(next) {}* };*/
class Solution {
public:ListNode* insertionSortList(ListNode* head) {ListNode* dummy = new ListNode(-1, head);ListNode* p = head->next;head->next = nullptr; // 刚开始已排序区间只有头节点,先将其 next 置为空标记排序区间的末尾while (p) {ListNode* cur = dummy;while (cur->next && cur->next->val <= p->val) cur = cur->next;ListNode* q = p->next;if (!cur->next) // p 比已排序节点都更大则接在已排序区间的末尾p->next = nullptr, cur->next = p;else // 否则 cur->next 是第一个大于 p 的节点,将 p 插入到 cur 后面p->next = cur->next, cur->next = p;p = q;}return dummy->next;}
};
LeetCode 148. 排序链表(中等)
【题目描述】
给你链表的头结点 head,请将其按升序排列并返回排序后的链表。
【示例 1】

输入:head = [4,2,1,3]
输出:[1,2,3,4]
【示例 2】

输入:head = [-1,5,3,4,0]
输出:[-1,0,3,4,5]
【示例 3】
输入:head = []
输出:[]
【提示】
链表中节点的数目在范围 [ 0 , 5 ∗ 1 0 4 ] [0, 5 * 10^4] [0,5∗104] 内
− 1 0 5 < = N o d e . v a l < = 1 0 5 -10^5 <= Node.val <= 10^5 −105<=Node.val<=105
进阶:你可以在 O ( n l o g n ) O(n log n) O(nlogn) 时间复杂度和常数级空间复杂度下,对链表进行排序吗?
【分析】
由于快排和递归的归并排序都需要递归,空间复杂度为 O ( l o g n ) O(log n) O(logn),只有迭代的归并排序可以实现 O ( 1 ) O(1) O(1) 的空间复杂度。
用迭代实现归并排序其实就是自底向上做,即刚开始的时候每个节点自身就是一个独立的区间。
第一次迭代的时候将每个长度为 1 的区间两两进行合并,成为一个长度为 2 的有序区间,然后下一轮就将每个长度为 2 的区间合并成长度为 4 的区间,以此类推。
本题的代码实现比较复杂,不太理解可以画个图模拟一下。
【代码】
/*** Definition for singly-linked list.* struct ListNode {* int val;* ListNode *next;* ListNode() : val(0), next(nullptr) {}* ListNode(int x) : val(x), next(nullptr) {}* ListNode(int x, ListNode *next) : val(x), next(next) {}* };*/
class Solution {
public:ListNode* sortList(ListNode* head) {int n = 0; // 链表长度for (ListNode* p = head; p; p = p->next) n++;for (int i = 1; i < n; i *= 2) { // 枚举要合并的每一段长度ListNode *dummy = new ListNode(-1),*cur = dummy; // dummy->next 是合并后上一层的头节点for (int j = 0; j < n; j += i * 2) { // 需要合并的次数为 (n + 1) / i * 2ListNode *p = head, *q = head;for (int k = 0; k < i && q; k++) q = q->next; // q 向后跳 i 次到另一段的头部int l = 0, r = 0; // 左右两段已合并的节点数while (l < i && r < i && p && q) { // 只要两段都不为空且还有节点没合并则进行对比合并if (p->val <= q->val) cur = cur->next = p, p = p->next, l++;else cur = cur->next = q, q = q->next, r++;}while (l < i && p) cur = cur->next = p, p = p->next, l++; // 合并左段剩余的节点while (r < i && q) cur = cur->next = q, q = q->next, r++; // 合并右段剩余的节点if (q) head = q; // head 移动到后面两段区间的头部}cur->next = nullptr; // 合并完成后将末尾节点的 next 置为空head = dummy->next;}return head;}
};
LeetCode 149. 直线上最多的点数(困难)
【题目描述】
给你一个数组 p o i n t s points points,其中 p o i n t s [ i ] = [ x i , y i ] points[i] = [x_i, y_i] points[i]=[xi,yi] 表示 X-Y 平面上的一个点。求最多有多少个点在同一条直线上。
【示例 1】

输入:points = [[1,1],[2,2],[3,3]]
输出:3
【示例 2】

输入:points = [[1,1],[3,2],[5,3],[4,1],[2,3],[1,4]]
输出:4
【提示】
1 < = p o i n t s . l e n g t h < = 300 1 <= points.length <= 300 1<=points.length<=300
p o i n t s [ i ] . l e n g t h = = 2 points[i].length == 2 points[i].length==2
− 1 0 4 < = x i , y i < = 1 0 4 -10^4 <= x_i, y_i <= 10^4 −104<=xi,yi<=104
points 中的所有点互不相同
【分析】
任意两点确定一条直线,我们可以先枚举每条直线,如果暴力枚举时间是 O ( n 2 ) O(n^2) O(n2),然后再判断有多少个点在这条直线上,时间为 O ( n ) O(n) O(n),因此总共的时间复杂度为 O ( n 3 ) O(n^3) O(n3)。
也可以枚举每个点,然后判断其他点到这个点的斜率是多少,也就是确定其他点与这个点所形成的直线,然后判断哪条直线上的点最多。由于垂直线没有斜率,因此可以用一个变量单独记一下。本题保证每个点不同,如果可能存在重复点那么还需要开个变量记录下相同点的数量,无论是哪条直线都要算上当前枚举点的重复点数量。
【代码】
class Solution {
public:int maxPoints(vector<vector<int>>& points) {int res = 0;for (auto a: points) {unordered_map<long double, int> cnt; // long double 防止精度被卡int vc = 0; // 与 a 在一条垂线上的点数for (auto b: points) {if (b == a) continue;if (b[0] == a[0]) vc++;else {long double k = (long double) (b[1] - a[1]) / (b[0] - a[0]); // 记得要强制转换cnt[k]++;}}for (const auto &[k, v]: cnt) res = max(res, v + 1);res = max(res, vc + 1);}return res;}
};
LeetCode 150. 逆波兰表达式求值(中等)
【题目描述】
给你一个字符串数组 tokens,表示一个根据逆波兰表示法表示的算术表达式。
请你计算该表达式。返回一个表示表达式值的整数。
注意:
- 有效的算符为
'+'、'-'、'*'和'/'。 - 每个操作数(运算对象)都可以是一个整数或者另一个表达式。
- 两个整数之间的除法总是 向零截断 。
- 表达式中不含除零运算。
- 输入是一个根据逆波兰表示法表示的算术表达式。
- 答案及所有中间计算结果可以用 32 位 整数表示。
【示例 1】
输入:tokens = ["2","1","+","3","*"]
输出:9
解释:该算式转化为常见的中缀算术表达式为:((2 + 1) * 3) = 9
【示例 2】
输入:tokens = ["4","13","5","/","+"]
输出:6
解释:该算式转化为常见的中缀算术表达式为:(4 + (13 / 5)) = 6
【示例 3】
输入:tokens = ["10","6","9","3","+","-11","*","/","*","17","+","5","+"]
输出:22
解释:该算式转化为常见的中缀算术表达式为:((10 * (6 / ((9 + 3) * -11))) + 17) + 5
= ((10 * (6 / (12 * -11))) + 17) + 5
= ((10 * (6 / -132)) + 17) + 5
= ((10 * 0) + 17) + 5
= (0 + 17) + 5
= 17 + 5
= 22
【提示】
1 < = t o k e n s . l e n g t h < = 1 0 4 1 <= tokens.length <= 10^4 1<=tokens.length<=104
tokens[i] 是一个算符("+"、"-"、"*" 或 "/"),或是在范围 [ − 200 , 200 ] [-200, 200] [−200,200] 内的一个整数
逆波兰表达式:
逆波兰表达式是一种后缀表达式,所谓后缀就是指算符写在后面。
- 平常使用的算式则是一种中缀表达式,如
( 1 + 2 ) * ( 3 + 4 )。 - 该算式的逆波兰表达式写法为
( ( 1 2 + ) ( 3 4 + ) * )。
逆波兰表达式主要有以下两个优点:
- 去掉括号后表达式无歧义,上式即便写成
1 2 + 3 4 + *也可以依据次序计算出正确结果。 - 适合用栈操作运算:遇到数字则入栈;遇到算符则取出栈顶两个数字进行计算,并将结果压入栈中。
【分析】
很经典的逆波兰表达式求值,提示中已经说明了做法,就是遇到数字就直接入栈,遇到运算符就出栈两个元素进行运算后将结果入栈,只要注意后出栈的那个才是被运算数,例如按顺序出栈 x x x 和 y y y,当前操作符为 /,那么运算结果为 y / x y / x y/x。
【代码】
class Solution {
public:int evalRPN(vector<string>& tokens) {stack<int> stk;for (string s: tokens) {if (s != "+" && s != "-" && s != "*" && s != "/") stk.push(stoi(s));else {int x = stk.top(); stk.pop();int y = stk.top(); stk.pop();if (s == "+") stk.push(y + x);else if (s == "-") stk.push(y - x);else if (s == "*") stk.push(y * x);else stk.push(y / x);}}return stk.top();}
};


靶场渗透)


