1.区间估计
(1)基本概念

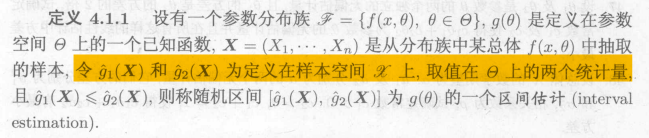
由于统计量的性质,每次取样的区间都是不一样的

我们希望可靠度尽可能的高的同时精度也尽可能的高,但往往这两者是矛盾的,不可以同时得到,于是我们希望在保证可靠度的基础上来使精度尽可能高。

对于置信区间的解释:
则为使用100次,平均大约有95次随机区间包含真实未知参数
,大约有5次随机区间
不包含真实未知参数
。



(3)进行区间估计的方法
a.Neyman置信区间(枢轴变量法)
b.Fisher信仰推断法
c.容忍区间,容忍限
d.Bayes方法
2.正态总体的枢轴变量法
如何寻找枢轴变量:
a.寻找待估参数的一个优良的点估计(一般是UMVUE)
b.构造优良的点估计和待估参数的一个函数,该函数的分布与待估参数无关。
说明:
由于分布与待估参数无关,那么很容易计算概率并与置信水平比较。
由于是优良的点估计和待估参数的一个函数,那么可以将待估参数移到不等式中间,于是不等式两边就都是统计量。
单正态总体:
总体服从正态分布,样本i.i.d正态分布
(1)单正态总体均值的估计
此时总体不必正态。
由于概率是对称的,所以取对称区间是区间最短,即精度最高的
(2)单正态总体方差的估计

n个标准正态分布的和

的分布
两个正态总体的区间估计:
总体之间独立,样本之间独立
(1)均值差的区间估计
最后一种情况总体不必正态。
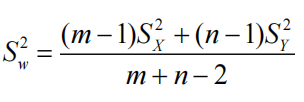

m=n的情况下使用如上方法是不合理,因为不知道X与Y的对应关系,如果知道,那么就可以
(2)方差比的区间估计



均值的置信限:
上限和下限
单正态总体均值和双正态总体均值差的总结:
均值/均值差d,其中d根据情况不同
对于置信限:只需要将改为
即可,
即为:
上限:
下限:
此时总体不必正态。
双正态总体是同样的。
同时均值是比方差更加敏感的
3.非正态总体的枢轴变量法
(1)指数分布


(2)均匀分布

(3)大样本方法
a.柯西分布
![]()
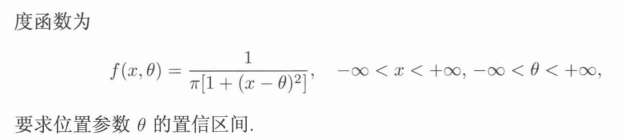
b.二项分布


上面的区间精度更高

c.泊松分布

此时需要更多的样本,因为进行了两次近似


d.一般情况下

相关例题:
例1:

指数族的自然形式

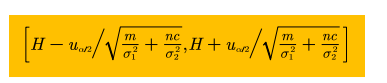
例2:

下限是大于等于号,但是未知参数在分母,所以得先小于
例3:


不等且未知
例4:


例5:


例6:
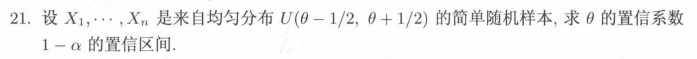


例7:

例8:


例9:


例10:
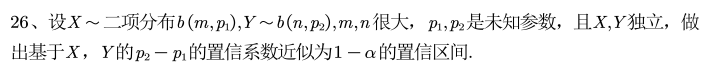




的语法着色文件)

)
