剑指Offer（数据结构与算法面试题精讲）C++版——day18

题目一：所有大于或等于节点的值之和

    题目：给定一棵二叉搜索树，请将它的每个节点的值替换成树中大于或等于该节点值的所有节点值之和。假设二叉搜索树中节点的值唯一。例如，输入如图8.10（a）所示的二叉搜索树，由于有两个节点的值大于或等于6（即节点6和节点7），因此值为6节点的值替换成13，其他节点的值的替换过程与此类似，所有节点的值替换之后的结果如图8.10（b）所示。
    由题意可知，这里其实是找一个二叉搜索树序列顺序遍历过程中，顶点值大于当前节点的所有节点和。有一种暴力实现思路，直接存储一遍按照中序遍历得到的节点值序列，然后再遍历一次，在数组中统计出现在当前节点之后的节点和。但是由于涉及到了数组遍历求和，所以这里的时间复杂度比较高。
    分析可以发现，如果倒着遍历，那么就能一次遍历，维护一个sum值，就能一次遍历拿到所有大于等于当前节点的所有节点和了。于是立马想到前面提到的二叉树中序遍历的非递归方式。可以借助于栈结构，先找到最右侧节点，然后访问中间“根节点”，再以相同的方式遍历左子树。于是得到如下代码：

void getBiggerSum(treeNode* tree) {treeNode* current=tree;stack<treeNode* > st;int sum=0;while(current||!st.empty()) {while(current) {st.push(current);current=current->right;//先找最右下角节点}current=st.top();st.pop();sum+=current->val;current->val=sum;current=current->left;}
}

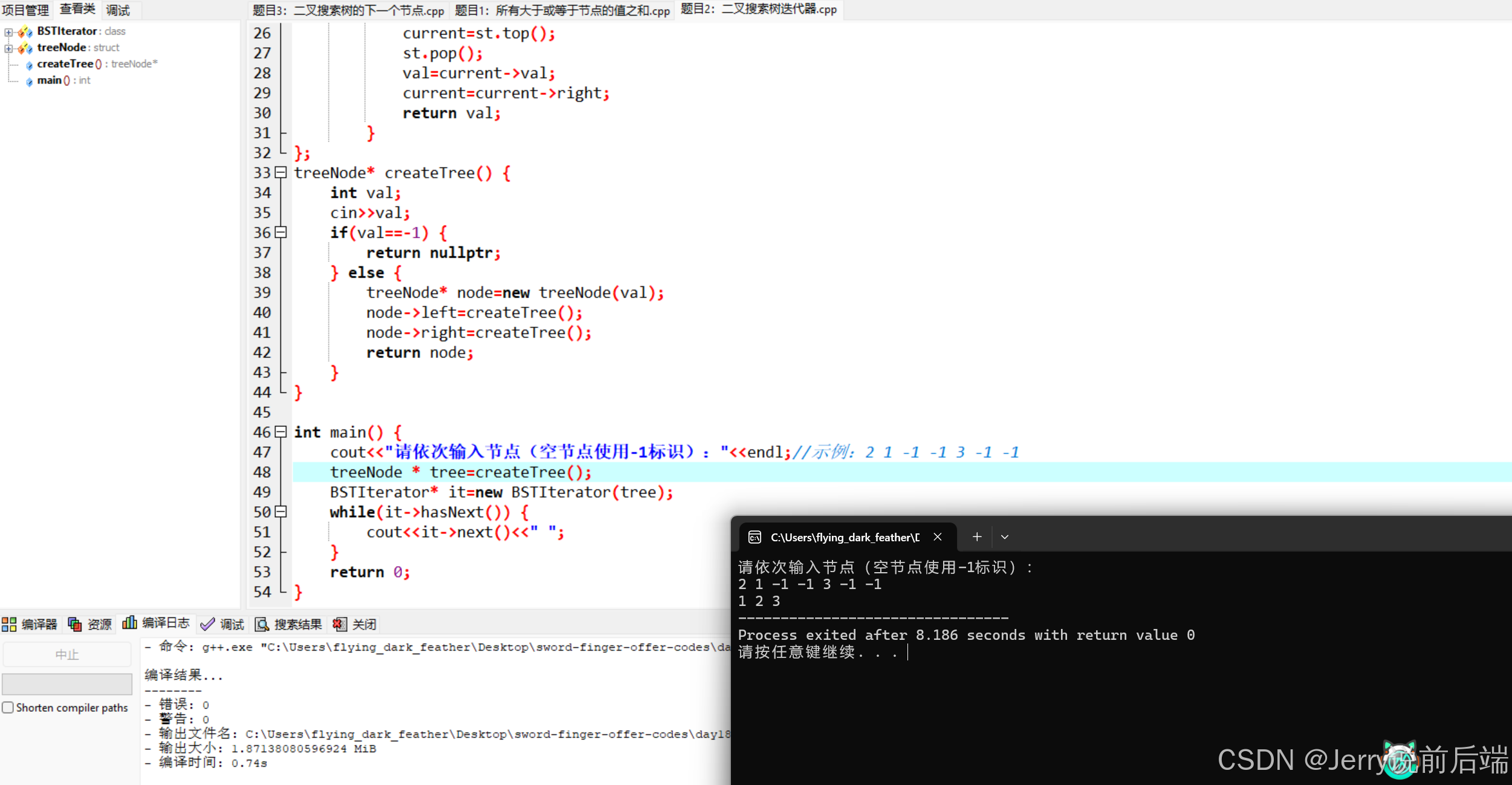
题目二：二叉搜索树迭代器

    题目：请实现二叉搜索树的迭代器BSTIterator，它主要有如下3个函数。
● 构造函数：输入二叉搜索树的根节点初始化该迭代器。
● 函数next：返回二叉搜索树中下一个最小的节点的值。
● 函数hasNext：返回二叉搜索树是否还有下一个节点。
    例如，输入图8.11中的二叉搜索树初始化BSTIterator，第1次调用函数next将返回最小的节点的值1，此时调用函数hasNext返回true。第2次调用函数next将返回下一个节点的值2，此时再调用函数hasNext将返回true。第3次调用函数next将返回下一个节点的值3，此时再调用函数hasNext将返回false。

    前端也有迭代器这个概念，要求能够拿到next之后标记新的位置，通过n次调用next能够将这个树完整完成一次遍历。可以发现如果不要求维持原来的树结构不变的话，那么可以构建一棵展平的树，只包含右侧节点，就类似于前面剑指Offer（数据结构与算法面试题精讲）C++版——day17中的题目二，这样直接获取一次右子节点就能够判断是否还有下一个节点。这样构建树时需要的时间复杂度为O(n)，next和hasNext判断只需要O(1)的时间复杂度。
    因为前面已经实现过这种代码，并且实际应用中往往不会轻易直接修改二叉树，如果改为创建一个展平二叉树副本，那么需要的空间复杂度为O(n)。这里给出一种利用栈和非递归中序遍历的方式实现。相当于将中序遍历的步骤拆解，同时记录被出输出节点的位置，这样就不需要构建一颗二叉树，同时栈的空间复杂度也小于直接创建副本的空间复杂度。得到的代码如下：

class BSTIterator {public:treeNode * current=nullptr;stack<treeNode* > st;BSTIterator(treeNode * tree) {current=tree;}bool hasNext() {return current||!st.empty();}int next() {int val=0;while(current) {st.push(current);current=current->left;}current=st.top();st.pop();val=current->val;current=current->right;return val;}
};

题目三：二叉搜索树中两个节点的值之和

    题目：给定一棵二叉搜索树和一个值k，请判断该二叉搜索树中是否存在值之和等于k的两个节点。假设二叉搜索树中节点的值均唯一。例如，在如图8.12所示的二叉搜索树中，存在值之和等于12的两个节点（节点5和节点7），但不存在值之和为22的两个节点。

    这个题目其实有点似曾相识，因为整体上由于是一颗二叉搜索树，那么中序遍历能够拿到一个递增的序列，那么立马会想到前面剑指Offer（数据结构与算法面试题精讲）C++版——day2中的题目三，也就是双指针法，用一个指针从左侧开始遍历，一个指针从右侧开始遍历。如果这两个指针指向的元素的和大于目标和，那么右指针左移，如果小于，则将左指针后移。问题的关键在于如何高效拿到前一个节点和后一个节点。
    由于前面的题目二中我们构建了一个后序迭代器，并且前面的题目一我们还设计过二叉搜索树的倒叙遍历方式，因此可以将题目一改造一下，同样设计一个找前一个节点的迭代器。这样就能还原为day2中的题目三了，然后高效处理这个问题。最终得到的代码如下：

bool checkExist(treeNode * tree,int sum) {BSTIterator* it=new BSTIterator(tree);BSTIteratorReverse* itReverse=new BSTIteratorReverse(tree);int first=it->next();int last=itReverse->pre();while(first!=last) {if(first+last==sum){return true;}else if(first+last>sum) {last=itReverse->pre();}else{first=it->next();}}return false;
}

附录：源码gitee仓库

    考虑到有些算法需要模拟数据，如果全部放进来代码显得过长，不利于聚焦在算法的核心思路上。于是把所有的代码整理到了开源仓库上，如果想要看详细模拟数据，可在开源仓库自取：【凌空暗羽/剑指Offer-C++版手写代码】。

    我是【Jerry说前后端】，本系列精心挑选的算法题目均基于经典的《剑指 Offer（数据结构与算法面试题精讲）》。在如今竞争激烈的技术求职环境下，算法能力已成为前端开发岗位笔试考核的关键要点。通过深入钻研这一系列算法题，大家能够系统地积累算法知识和解题经验。每一道题目的分析与解答过程，都像是一把钥匙，为大家打开一扇通往高效编程思维的大门，帮助大家逐步提升自己在数据结构运用、算法设计与优化等方面的能力。
    无论是即将踏入职场的应届毕业生，还是想要进一步提升自身技术水平的在职开发者，掌握扎实的算法知识都是提升竞争力的有力武器。希望大家能跟随我的步伐，在这个系列中不断学习、不断进步，为即将到来的前端笔试做好充分准备，顺利拿下心仪的工作机会！快来订阅吧，让我们一起开启这段算法学习之旅！