声明：本篇文章需要较高版本的r,最好4以上，否则一些函数没法用。
一、数据的长宽变换
r语言进行重复测量方差分析需要使用长型数据，而spss进行重复测量方差分析则需要使用宽型数据
1.长数据变为宽数据
首先，生成数列
其次，安装tidyr包
install.packages("tidyr")
library(tidyr)
spread(df, Time, R)
2.宽数据变为长数据
install.packages("reshape2")
library(reshape2)
aa<-melt(a, id.vars=c("Sub"), variable.name=c("Time"),value.name=c("R"))
melt(data,id.vars,measure.vars,variable.name=“variable”,…,na.rm=FALSE,value.name=“value”,
factorsAsStrings=TRUE)
ps:发现查找函数意义的一个新方法:
data,数据
id.vars:你不想改变的数据列
measure.vars：你要melt的数据
variable.name：melt操作后，为新列变量取名
value.name：新列对应值的变量名
如果不命名：
二、单因素方差分析
首先。生成数据
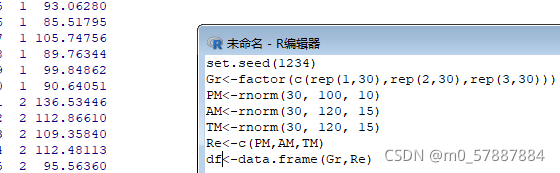
在进行方差分析之前要进行方差齐性检验
install.packages("DescTools")
library(DescTools)
LeveneTest(Re ~ Gr, data=df)
方差齐性假设的原假设是两个样本的方差是齐性的，如果p<0.05的话，说明拒绝原假设，两个样本方差不齐，如果p>0.05的话，说明接受原假设，两者方差齐性，可以进行下一步的分析。
因此，我们进行方差分析。
model1<-aov(Re ~ Gr, data=df)
anova(model1)
自变量写在~右边，因变量写在~左边
p<0.05，因此是显著的（e^-10=0.000045.....），可以进行下一步的分析
F检验显著说明各组均值并不相同，但不能说明到底那几组不同，因此要进行事后比较，通过对各组均值之间的配对比较来进一步检验到底哪些均值之间存在差异。
事后多重比较的方法有许多，比如LSD,Bonferroni等，其中，LSD(最小差异显著法）是最灵敏的事后多重比较的方法，各种事后比较方法灵敏度排名如下：
LSD法>Sidak法>Bonferroni法>Scheffe法>Dunnett法。
事后检验的方法如下：
library(DescTools)
PostHocTest(model1, method="bonferroni")
结果如下：
两两差异显著。
由于推论统计上的显著并不一定意味着实际效果的显著，结果显著不一定是由自变量造成的，因此需要计算效应量。
效应量是不依赖于样本大小，反应自变量与因变量关联程度的指标。
评价效应量大小的标准：当对两个独立组平均只差进行显著性检验时，可以使用d和点二列相关系数的平方r²作为效应量。d=0.2:效果小；d=0.5,(效果一般）；d=0.8（效果很好）
r²=0.2:效果小）；r²=0.5：效果一般；r²=0.8,效果很好
当使用方差分析时，可以使用η²， ω ²。η²在样本范围内使用，ω ²在总体范围内使用。
η²越大，说明自变量效果越大，自变量对因变量越重要。
ω ²<6%：变量间关系微弱
6%<ω ²<6%：变量间关系中等
ω ²>16%:变量间关系比较强
