【因果推断python】46_估计量2

连续型干预变量案例

非线性处理效果

关键思想

连续型干预变量案例

目标转换方法的另一个明显缺点是它仅适用于离散或二元处理。这是你在因果推理文献中经常看到的东西。大多数研究都是针对二元干预案例进行的，但您找不到很多关于连续干预的研究。这让我很困扰，因为在这个行业中，持续干预无处不在，主要是您需要优化的价格形式。因此，即使我找不到任何关于持续干预的目标转换的信息，我还是想出了一些在实践中有效的方法。请记住，我没有围绕它进行的超级可靠的计量经济学研究。

为了激发它，让我们回到冰淇淋销售的例子。在那里，我们的任务是估计价格的需求弹性，以便我们可以更好地设定冰淇淋价格以优化我们的收入。回想一下，数据集中的事件样本是一天，我们希望知道人们何时对价格上涨不那么敏感。另外，回想一下，价格在这个数据集中是随机分配的，这意味着我们不需要担心混淆偏差。

prices_rnd = pd.read_csv("./data/ice_cream_sales_rnd.csv")
prices_rnd.head()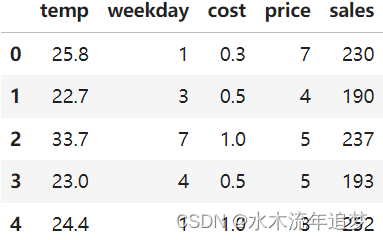

和之前一样，让我们先把数据分为训练和测试两个集合。

np.random.seed(123)
train, test = train_test_split(prices_rnd, test_size=0.3)
train.shape, test.shape
((3500, 5), (1500, 5))

现在是我们需要一点创造力的地方。对于离散情况，条件平均处理效果由当我们从未处理到处理时结果变化多少给出，以单位特征 X 为条件。

$\tau(x)=E[Y_i(1)-Y_i(0)|X]=E[\tau_i|X]$

简而言之，这是估计处理对不同单元配置文件的影响，其中配置文件是使用特征 X 定义的。对于连续的情况，我们没有那个开关。单元未经处理或未经处理。相反，它们都经过处理，但强度不同。因此，我们不能谈论给予干预的效果。相反，我们需要从增加干预的角度说话。换句话说，我们想知道如果我们增加一定量的干预，结果会如何变化。这就像估计结果函数 Y 对干预 t 的偏导数。并且因为我们希望知道对于每个组（CATE，而不是 ATE），我们以特征 X 为条件

$\tau(x)=E[\partial Y_i(t)|X]=E[\tau_i|X]$

我们如何估计呢？首先，让我们考虑一个简单的情况，其中结果与干预呈线性关系。假设您有两种类型的日子：炎热的日子（黄色）和寒冷的日子（蓝色）。在寒冷的日子里，人们对价格上涨更加敏感。此外，随着价格上涨，需求线性下降。

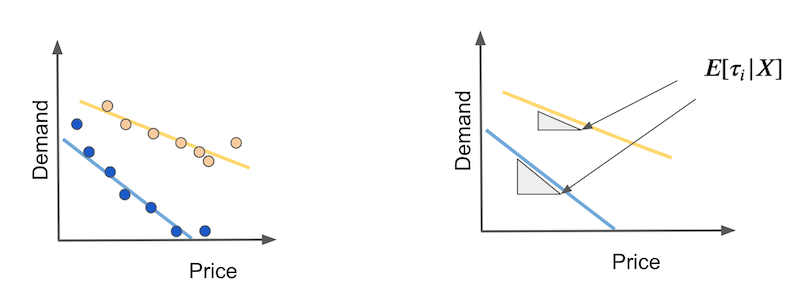
在这种情况下，CATE 将是每条需求线的斜率。这些斜率将告诉我们，如果我们将价格提高任何数量，需求会下降多少。如果这种关系确实是线性的，我们可以分别用简单线性回归估计热天和冷天的系数来估计这些弹性。

我们可以从这个估算器中得到启发，思考一个单独的单元会是什么样子。换句话说，如果我们在那里有同样的东西，为每一天定义。在我的脑海里，它会是这样的：

$Y_i^*=(Y_i-\bar{Y})\frac{(T_i-\bar{T})}{\sigma_T^2}$

用简单的英语来说，我们将通过从中减去平均值来转换原始目标，然后将其乘以处理，我们也从中减去了平均值。最后，我们将其除以处理方差。唉，我们有一个针对连续情况的目标转换。

现在的问题是：它有效吗？事实上，它确实如此，我们可以通过一个类似的证明来证明它为什么起作用，就像我们在二进制案例中所做的那样。首先，让我们打电话

$V_i=\frac{(T_i-\bar{T})}{\sigma_T^2}$

注意 $E[V_i|X_i=x]=0$ a 因为在随机分配下 $E[T_{i}|X_{i}=x]=\bar{T}$ 。换句话说，对于 X 的每个区域， $E[T_{i}]=\bar{T}$ 。还有 $E[T_iV_i|X_i=x]=1$ 因为 $E[T_i(T_i-\bar{T})|X_i=x]=E[(T_i-\bar{T})^2|X_i=x]$ ，即处理方差。最后，在条件独立（我们在随机处理分配情况下免费获得）下， $E[T_ie_i|X_i=x]=E[T_i|X_i=x]E[e_i|X_i=x]$ 。

为了证明这个目标转换是有效的，我们需要记住我们正在估计一个局部线性模型的参数

$Y_i=\alpha+\beta T_i+e_i|X_i=x$

在我们的示例中，这些将是炎热和寒冷日子的线性模型。在这里，我们对 $\beta$ 参数感兴趣，这是我们的条件弹性或 CATE。有了这一切，我们可以证明

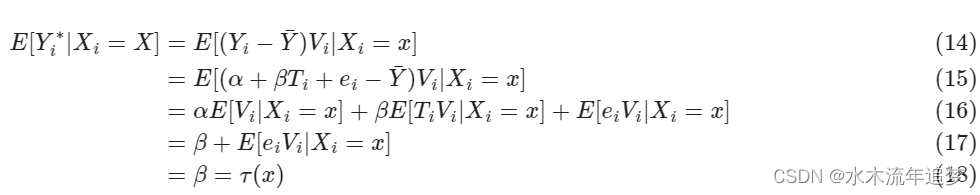
请记住，这仅在随机干预时有效。对于非随机处理，我们必须将 $\bar{T}$ 替换为 $M(X_{i})$ ，其中 M 是一个估计 $E[T_i|X_i=x]$ 。

$Y_i^*=(Y_i-\bar{Y})\frac{(T_i-M(T_i))}{(T_i-M(T_i))^2}$

这将确保第三行中的 $\alpha E[V_i|X_i=x]$ 消失为零，并且 $E[T_iV_i|X_i=x]$ 消失到 1。请注意，如果您只想根据干预效果对单位进行排序，实际上并不需要 $E[T_iV_i|X_i=x]$ 去 1。换句话说，如果您只想知道需求在哪几天对价格上涨更敏感，但您不需要知道多少，那么 $\beta$ 估计值是否按比例缩放并不重要上或下。如果是这种情况，您可以省略分母。

$Y_i^*=(Y_i-\bar{Y})(T_i-M(T_i))$

如果所有这些数学看起来很烦人，请不要担心。代码其实很简单。再一次，我们用上面看到的公式转换我们的训练目标。在这里，我们有随机的处理分配，所以我们不需要建立一个预测价格的模型。我也省略了分母，因为这里我只关心排序处理效果。

y_star_cont = (train["price"] - train["price"].mean()*train["sales"] - train["sales"].mean())#然后，就像以前一样，我们拟合回归 ML 模型来预测该目标。
cate_learner = LGBMRegressor(max_depth=3, min_child_samples=300, num_leaves=5)np.random.seed(123)
cate_learner.fit(train[["temp", "weekday", "cost"]], y_star_cont)cate_test_transf_y = cate_learner.predict(test[["temp", "weekday", "cost"]])test_pred = test.assign(cate=cate_test_transf_y)
test_pred.sample(5)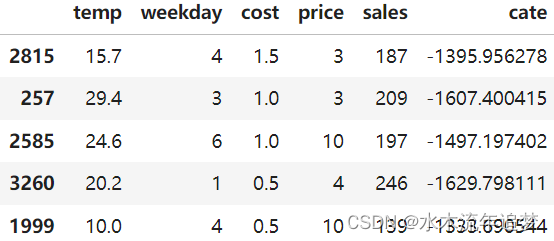

这一次，CATE 的解释是不直观的。由于我们已经从目标转换中删除了分母，所以我们看到的这个 CATE 是由 ��(�) 缩放的。然而，这个预测仍然应该很好地排序干预效果。为了看到这一点，我们可以使用累积增益曲线，就像我们之前所做的那样。

gain_curve_test = cumulative_gain(test.assign(cate=cate_test_transf_y),"cate", y="sales", t="price")gain_curve_train = cumulative_gain(train.assign(cate=cate_learner.predict(train[["temp", "weekday", "cost"]])),"cate", y="sales", t="price")plt.plot(gain_curve_test, label="Test")
plt.plot(gain_curve_train, label="Train")
plt.plot([0, 100], [0, elast(test, "sales", "price")], linestyle="--", color="black", label="Taseline")
plt.legend();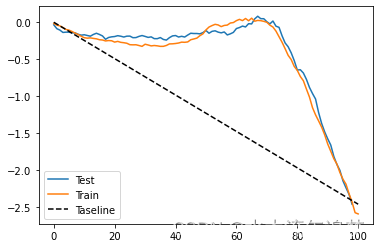

对于这些数据，看起来具有转换目标的模型比随机模型要好得多。不仅如此，训练和测试结果非常接近，因此这里的方差不是问题。但这只是这个数据集的一个特征。如果您还记得，当我们探索二元处理案例时，情况并非如此。在那里，模型的表现不是很好。

非线性处理效果

谈到了连续案例，我们需要处理的房间里还有一头大象。我们假设干预效果呈线性关系。然而，这很少是一个合理的假设。通常，干预效果以一种或另一种形式饱和。在我们的示例中，可以合理地认为，在价格上涨的第一个单位时需求会下降得更快，但随后会下降得更慢。

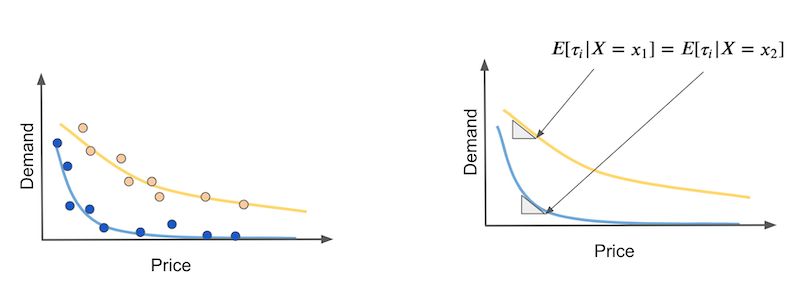
这里的问题是弹性或干预效果随干预本身而变化。在我们的示例中，干预效果在曲线开始时更加强烈，而随着价格的上涨而减弱。同样，假设您有两种类型的日子：炎热的日子（黄色）和寒冷的日子（蓝色），我们想用因果模型区分这两者。问题是因果模型应该预测弹性，但在非线性情况下，如果我们查看曲线中不同的价格点（右图），炎热和寒冷天的弹性可能相同。

解决这个问题没有简单的方法，我承认我仍在研究什么最有效。目前，我所做的事情是尝试考虑干预效果的函数形式，并以某种方式将其线性化。例如，需求通常具有以下函数形式，其中较高的 $\alpha s$ 意味着随着价格的每次上涨，需求下降得更快

$D_i=\frac1{P_i^\alpha}$

所以，如果我对需求 Y 和价格 T 都应用对数转换，我应该得到线性的东西。

线性化并不是那么容易做到的，因为它需要一些思考。但你也可以尝试一些东西，看看什么效果最好。通常，对数和平方根之类的东西会有所帮助。

关键思想

我们现在正朝着使用机器学习模型估计条件平均干预效果的方向发展。这样做的最大挑战是使预测模型适应估计因果效应的模型。另一种思考方式是，预测模型专注于将结果 Y 估计为特征 X 的函数，可能还有干预 T, $Y=M(X,T)$ 而因果模型需要估计这个输出函数在处理 $\partial Y=\partial M(X,T)$ 上。这不是简单方法就可以解决的，因为虽然我们确实观察到了结果 Y，但我们不能观察到 $\partial Y$ ，至少在个体样本层面上不能。因此，在为我们的模型设计目标函数时，我们需要具有创造性。

在这里，我们看到了一种非常简单的目标转换技术。这个想法是将原始目标 Y 与干预 T 结合起来，形成一个转换后的目标，期望它等于 CATE。有了这个新目标，我们可以插入任何预测性 ML 模型来估计它，然后模型预测将是 CATE 估计。附带说明一下，除了目标转换之外，此方法也称为 F-Learner。

尽管如此简单，但也需要付出代价。转换后的目标是对个体干预效果的非常嘈杂的估计，并且该噪声将以方差的形式转移到模型估计中。这使得目标转换更适合大数据应用，在这些场景中，由于样本量很大，方差不是个大问题。目标转换方法的另一个缺点是它仅针对二元或分类处理定义。我们尽最大努力提出该方法的连续版本，甚至最终得出了一些似乎可行的方法，但到目前为止，还没有可靠的理论框架来支持它。

最后，我们以对非线性干预效果及其带来的挑战的讨论结束。也就是说，当干预效果随干预本身而变化时，我们可能会错误地认为单位具有相同的干预反应曲线，因为它们对干预的反应相同，但实际上它们只是接受了不同的干预量。

【因果推断python】46_估计量2

连续型干预变量案例

非线性处理效果

关键思想

相关资讯

热文排行

最新新闻

推荐新闻

热搜词