蓝桥与力扣刷题（74 搜索二维矩阵）

题目：给你一个满足下述两条属性的 m x n 整数矩阵：

• 每行中的整数从左到右按非严格递增顺序排列。
• 每行的第一个整数大于前一行的最后一个整数。

给你一个整数 target ，如果 target 在矩阵中，返回 true ；否则，返回 false 。

示例 1：

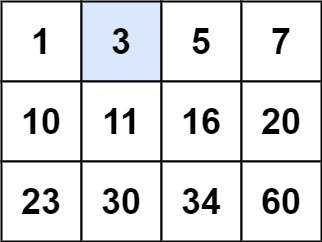
输入：matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 3
输出：true

示例 2：

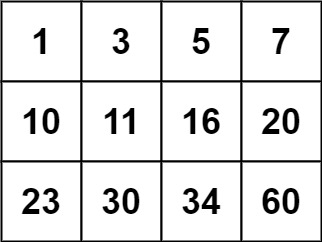
输入：matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 13
输出：false

提示：

• m == matrix.length
• n == matrix[i].length
• 1 <= m, n <= 100
• -104 <= matrix[i][j], target <= 104

解题思路＋代码：

代码：

class Solution {public boolean searchMatrix(int[][] matrix, int target) {int m = matrix.length; //矩阵行数if (m == 0) return false; int n = matrix[0].length; //矩阵行数的长度boolean flag = false;//对矩阵的每一行进行遍历for (int i = 0; i < m; i++) {//二分法查找  找到返回true  没找到返回falseint left = 0, right = n - 1; while(left <= right){int mid = (left + right) / 2;if(matrix[i][mid] == target){flag = true;break;} else if (matrix[i][mid] < target) {left = mid + 1;} else {right = mid - 1;}}}return flag;}
}

 总结：该题主要考察矩阵和二分法的运用。要解答该题，需要掌握矩阵与二分法的相关知识。通过二分查找，并与目标值进行匹配搜索效率会更快。这道题是对矩阵中的每一行进行二分查找，实际上也可以查找每一行的最后一个值，如果大于目标值，即锁定该行再继续二分查找。否则，一直往下一行查找，直到找到目标值，未找到返回结果。当然，这道题使用暴力枚举也可以，但是遇到非常大的矩阵，暴力枚举所花费的时间会比较久，因此不太推荐。