【PyTorch】PyTorch中的非线性激活函数详解：原理、优缺点与实战指南

- PyTorch中的非线性激活函数详解：原理、优缺点与实战指南
- - 一、核心激活函数作用、分类与数学表达
  - - 1. 传统饱和型激活函数
    - 2. ReLU族（加权和类核心）
    - 3. 自适应改进型激活函数
    - 4. 轻量化与硬件友好型
  - 二、优缺点对比与适用场景
  - 三、选择策略与PyTorch实现建议
  - 四、PyTorch代码示例
  - 五、选择策略与实战技巧
  - 六、总结

PyTorch中的非线性激活函数详解：原理、优缺点与实战指南

在深度学习中，激活函数是神经网络的核心组件之一，它决定了神经元的输出是否被激活，并赋予网络非线性建模能力。PyTorch提供了丰富的激活函数实现，本文将系统解析其数学原理、优缺点及适用场景，并给出实战建议。

一、核心激活函数作用、分类与数学表达

PyTorch的激活函数可分为以下四类，每类包含典型代表及其数学形式：

作用：

引入非线性：使网络能够学习复杂模式。
特征映射：将输入数据转换到新的特征空间。
梯度传播控制：通过导数影响权重更新。

分类：

饱和型（Sigmoid, Tanh）
ReLU族（ReLU, LeakyReLU, PReLU, ELU）
自适应型（Swish, GELU, SELU）
轻量型（ReLU6, Hardswish）

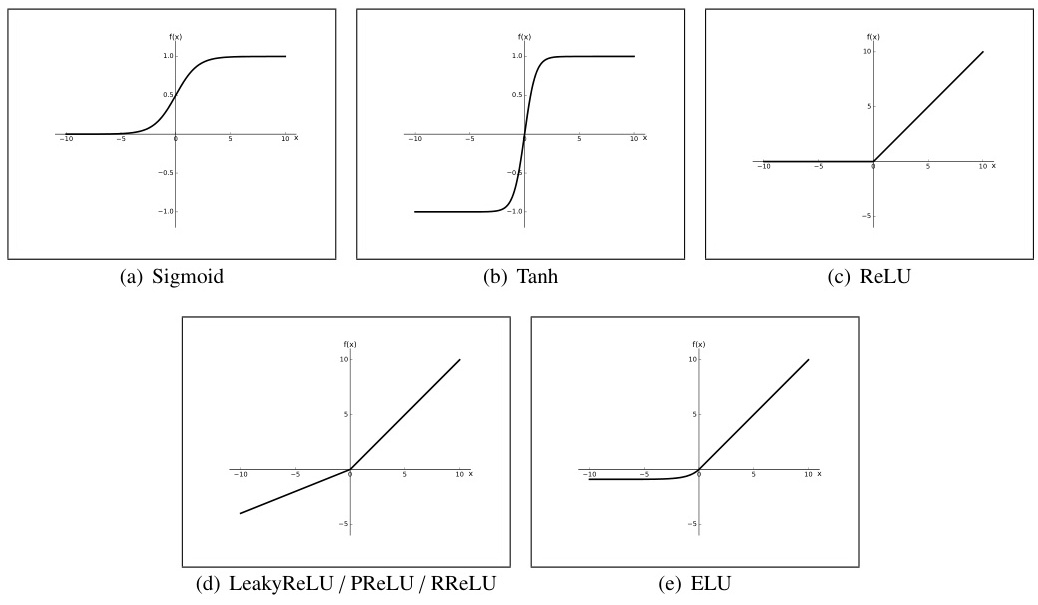
1. 传统饱和型激活函数

Sigmoid
$\frac{1}{1 + e^{-x}}$
特点：输出范围(0,1)，适合二分类输出层；缺点：梯度消失严重（导数最大仅0.25），输出非零中心化。
应用：二分类输出层、LSTM门控。
Tanh
$\tanh(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}}$
特点：输出范围(-1,1)，零中心化；缺点：梯度消失问题仍存在（最大导数1.0），指数计算成本较高。
应用：RNN隐藏层。

2. ReLU族（加权和类核心）

ReLU
$\text{ReLU}(x) = \max(0, x)$
特点：计算高效，稀疏激活；缺点：负区间神经元死亡（Dead ReLU），输出非零中心化。
应用：CNN隐藏层（默认选择）。
Leaky ReLU
$\text{LeakyReLU}(x) = \begin{cases} x & x \geq 0 \\ \alpha x & x < 0 \end{cases}$
特点：引入负区间斜率 $\alpha$ （通常0.01），缓解神经元死亡；缺点：需手动设定 $\alpha$ ，性能提升有限。
应用：替代ReLU的保守选择。
Parametric ReLU (PReLU)
$\text{PReLU}(x) = \begin{cases} x & x \geq 0 \\ \alpha x & x < 0 \end{cases}$ （ $\alpha$ 可学习）
特点：自适应调整负区间斜率，适合复杂任务；缺点：增加参数量。
Exponential Linear Unit (ELU)
$\text{ELU}(x) = \begin{cases} x & x \geq 0 \\ \alpha(e^x - 1) & x < 0 \end{cases}$
特点：负区间指数平滑，输出接近零中心化；缺点：计算复杂度略高。
应用：高鲁棒性要求的深度网络。

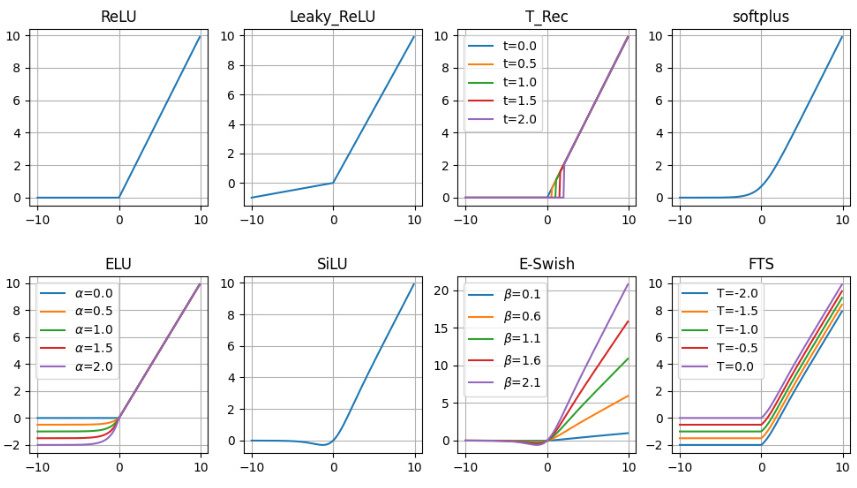
3. 自适应改进型激活函数

Swish
$\text{Swish}(x) = x \cdot σ(\beta x)$ （ $\beta$ 可调）
特点：平滑非单调，谷歌实验显示优于ReLU；缺点：计算量较大。
应用：复杂任务（如NLP、GAN）。
GELU
$\text{GELU}(x) = x \cdot \Phi(x)$ （ $\Phi(x)$ 为标准正态CDF）
特点：引入随机正则化思想（如Dropout），适合预训练模型；缺点：近似计算需优化。
应用：Transformer、BERT等预训练模型。
Self-Normalizing ELU (SELU)
$\text{SELU}(x) = \lambda \begin{cases} x & x \geq 0 \\ \alpha(e^x - 1) & x < 0 \end{cases}$
特点：自归一化特性（零均值、单位方差），适合极深网络；缺点：需配合特定初始化。
应用：自编码器、无监督学习。

4. 轻量化与硬件友好型

ReLU6
$\text{ReLU6}(x) = \min(\max(0, x), 6)$
特点：限制正区间梯度，防止量化误差（移动端模型）；缺点：牺牲部分表达能力。
应用：移动端模型（如MobileNet）。
Hardswish
$\text{Hardswish}(x) = x \cdot \frac{\min(\max(0, x+3), 6)}{6}$
特点：Swish的硬件优化版本，适合移动端；缺点：非线性较弱。
应用：移动端实时推理。

二、优缺点对比与适用场景

激活函数	优点	缺点	适用场景
Sigmoid	输出概率化，适合二分类输出层	梯度消失严重，非零中心化	二分类输出层，门控机制（如LSTM）
Tanh	零中心化，梯度略强于Sigmoid	梯度消失问题仍存在	RNN隐藏层
ReLU	计算高效，缓解梯度消失	神经元死亡，非零中心化	CNN隐藏层（默认选择）
Leaky ReLU	缓解Dead ReLU问题	需手动调参，性能提升有限	替代ReLU的保守选择
ELU	负区间平滑，噪声鲁棒性强	计算复杂度高	需要高鲁棒性的深度网络
Swish	平滑非单调，实验性能优异	计算成本较高	复杂任务（如NLP、GAN）
GELU	结合随机正则化，适合预训练	需近似计算	Transformer、BERT类模型
SELU	自归一化，适合极深网络	依赖特定初始化（lecun_normal）	无监督/自编码器结构
ReLU6	防止梯度爆炸，量化友好	表达能力受限	移动端部署（如MobileNet）

三、选择策略与PyTorch实现建议

隐藏层默认选择：优先使用ReLU或改进版本（Leaky ReLU、ELU），平衡性能与计算成本。
输出层适配：
- 二分类：Sigmoid
- 多分类：Softmax（LogSoftmax配合NLLLoss更稳定）
- 回归任务：线性激活或Tanh（输出范围限制）
极深网络优化：使用SELU配合自归一化初始化，或GELU增强非线性。
移动端部署：选择ReLU6或Hardswish，优化推理速度。
实践技巧：
- 对Dead ReLU问题，可尝试He初始化或加入BatchNorm。
- 使用nn.Sequential时，注意激活函数的位置（通常在卷积/线性层后）。

四、PyTorch代码示例

import torch.nn as nn# 定义含多种激活函数的网络
class Net(nn.Module):def __init__(self):super().__init__()self.fc = nn.Linear(784, 256)self.act1 = nn.ReLU()        # 默认ReLUself.act2 = nn.LeakyReLU(0.01)  # Leaky ReLUself.act3 = nn.SELU()        # SELU（需配合lecun_normal初始化）def forward(self, x):x = self.fc(x)x = self.act1(x)x = self.act2(x)return self.act3(x)

五、选择策略与实战技巧

隐藏层默认选择：
- 通用场景：优先使用ReLU，兼顾速度和性能。
- 深度网络：尝试GELU或SELU（配合自归一化初始化）。
- 稀疏梯度需求：使用LeakyReLU或ELU。
输出层适配：
- 二分类：Sigmoid（输出概率）。
- 多分类：Softmax（输出概率分布）。
- 回归任务：无激活（线性输出）或Tanh（限制范围）。
避免Dead ReLU：
- 使用He初始化（init.kaiming_normal_）。
- 加入Batch Normalization层。
- 设置适当的学习率（过大易导致神经元死亡）。
移动端优化：
- 选择ReLU6或Hardswish，减少浮点运算。
- 使用PyTorch的量化工具链（如TorchScript）。

代码示例：

import torch.nn as nn
import torch.nn.init as initclass DeepNetwork(nn.Module):def __init__(self):super().__init__()self.fc1 = nn.Linear(784, 256)self.act1 = nn.GELU()         # 使用GELUself.fc2 = nn.Linear(256, 128)self.act2 = nn.SELU()         # 使用SELU需配合特定初始化self._init_weights()def _init_weights(self):init.kaiming_normal_(self.fc1.weight, nonlinearity='gelu')init.lecun_normal_(self.fc2.weight)  # SELU推荐初始化def forward(self, x):x = self.act1(self.fc1(x))x = self.act2(self.fc2(x))return x