【深度学习—李宏毅教程笔记】机器学习任务攻略

一、为什么训练过程中用了 validation set ，模型还是过拟合了？

二、如果模型在测试集上的效果不理想，要做的是什么？

步骤一

步骤二

三、为什么要用 Validation set 呢？ Validation set 对模型的训练起了哪些贡献？让 test set 代替 Validation set 可以吗？

四、优化器（optimization）“不行” 的原因分析

五、训练技巧：Batch

六、梯度下降法的优化

七、分类任务为什么要用one-hot编码表示不同的类，而不用一些连续地数值代表不同的类？

八、为什么分类任务地损失函数更适合用交叉熵，而不是均方误差？

一、为什么训练过程中用了 validation set ，模型还是过拟合了？

在统计学习中，我们知道：

在训练集数据上进行训练，对于神经网络模型，相当于在一个无限的假设空间中选择一个最好的模型，如果只有这个，那么一定会过拟合，所以加入了正则化，并在 validation set 上对模型进行评估选择，如果模型在 validation set 上表现得不好，则需要进行调整，所以这相当于让模型在 validation set 数据集上进行了选择（这相当于让模型也在 validation set 数据集提供的假设空间上进行了选择，但这个假设空间比较小），所以模型也会慢慢地倾向于适合 validation set 数据集，最终导致模型对未知的 test set 的相对于训练集的未知领域的泛化能力并不是最大熵的。最终导致了轻微的过拟合。

下面是整理后的 AI 的回答：

在神经网络的训练过程中，虽然使用了验证集（validation set）来监控模型的性能，但模型依然可能出现过拟合现象。主要原因包括以下几个方面：

验证集的作用与局限性

监控作用，而非直接防止过拟合：验证集主要用于评估模型在未见数据上的表现，以便调整超参数和决定何时停止训练（例如早停策略）。它并不直接参与梯度更新，也不会对模型参数施加正则约束，所以仅依赖验证集监控并不能完全避免模型对训练数据的过拟合。

过度依赖验证集结果进行超参数调整：如果在模型的设计和超参数调整过程中反复使用验证集的信息，可能会导致“ validation set 集泄露”，使得模型在验证集上表现得更好，但在真正的测试集或新数据上依然表现不佳。

过度调整超参数
反复试验引发验证集信息泄露：在模型开发过程中，通过反复试验不断调整模型的结构与超参数，模型可能“学会”了验证集的某些特性，从而使得在验证集上表现看似优异但泛化能力有限。

二、如果模型在测试集上的效果不理想，要做的是什么？

步骤一

首先，查看模型在训练集（train data）上是否学好，如果在训练集上也没有学好，有两个可能：

（1）模型偏差（model bias）的问题

什么是 model bias ？即模型不适合，比如说选择的模型太过简单了，怎么办呢？重新设计模型，提升模型复杂度（或者说：假设空间放大 / 给模型更大的弹性）。

（2）优化器（optimization）选择的不好

优化器不能找到假设空间中最好的假设（或者说不能找到最好的模型）。

例子：

对于这个图中的例子，56 层的网络测试误差更大，这就一定是过拟合了吗？不一定，要看在训练集上的误差，如下图：

56 层在训练集上的效果也不好，所以说一定不是过拟合，一定是优化器的问题，因为在测试集上。如果说优化器没有问题，那么更复杂的模型的误差一定是小于简单模型的。

步骤二

解决了训练误差的问题，即训练误差很小，如果测试误差也变小了，那么就解决了这个问题。如果测试误差仍然很大，那么问题是什么呢？有两种可能：

（1）过拟合（overfitting）

对过拟合的解释略。

解决过拟合的方式：

方法一：数据增强（data augmentation）

对于图片数据来说，可以对图像：左右翻转、放大、缩小等正常的操作，不能随意做数据增强，即不能上下翻转，因为实际中对于反着的物体不常见。

方法二：对模型进行限制（削减假设空间 / 削减模型弹性）

CNN 模型相对于全连接网络所作的优化就是对模型进行限制，削减了一部分假设空间，但留下的正是恰好适合图像的部分。

方法三：早停（early stopping）

方法四：正则化（regularization）

它和方法二有联系

（2）数据分布不一致（Data Distribution Mismatch）

训练集和测试集的数据分布不同，导致模型在训练集上学到的模式无法适应测试集。这个现象有人也称其为 overfitting，但它不能通过收集更多的 train set 来解决。

原因：
- 训练集和测试集来自不同的来源或时间段（例如，训练集来自某个地区的数据，而测试集来自另一个地区的数据）。
- 数据预处理或特征工程在训练集和测试集之间没有一致应用，导致测试集和训练集在特征尺度、特征选择等方面不同。
- 测试集数据包含训练数据中没有出现过的情况或样本，导致模型无法应对这些新情况。
解决方法：
- 确保训练集和测试集来自相同的分布，尽可能地保证数据采样的一致性。
- 使用 标准化 或 归一化 等技术处理数据，以确保数据在训练和测试集之间的一致性。
- 尝试使用 交叉验证 来确保模型在不同数据集上的性能稳定。

三、为什么要用 Validation set 呢？ Validation set 对模型的训练起了哪些贡献？让 test set 代替 Validation set 可以吗？

表面上看， Validation set 好像并没有参与训练，但其实不然，模型的训练受到 Validation set 的监督，训练过程中我们会人为得选择更适合 Validation set 的模型，这就导致了 Validation set 间接地参与了模型的训练，从而 Validation set 中的信息被泄露到了训练过程中，如果让 test set 的数据作为 Validation set 就会导致模型即使在 test set（公共public测试数据集）上很好，但当使用模型时，他在 “私人private数据集上效果很差” 。当我们在 train set 上分出一部分作为 Validation set 时，在训练过程中，完全没有 public test set 的身影，这时 public test set 就可以认为是 private test set 了。

四、优化器（optimization）“不行” 的原因分析

原因：梯度下降时的梯度为 0（临界点 critical point）

有两种情况：局部极小值（local minima）、鞍点（saddle point），但更可能是第二种，第一种的可能性很小。

如何判别临界点是局部极小值还是鞍点呢？

在临界点附近，损失函数可用二阶近似来表示：

$L(\theta) \approx L(\theta') + (\theta - \theta')^T g + \frac{1}{2} (\theta - \theta')^T H (\theta - \theta')$

第二项中的 g 是梯度，在临界点处为 0 ，第三项的 H 是黑塞矩阵，它反映的是在临界点处的曲率。

到这里，很明显可以感觉到，有了临界点处的曲率信息，就能很轻易地判别临界点是局部极小值还是鞍点了，如果黑塞矩阵地特征值都大于 0（黑塞矩阵是正定的），那么损失函数在临界点处所有方向的曲率都大于0，就可以判定这个点就是局部极小值；如果黑塞矩阵的特征值有小于 0 的，就说明损失函数在临界点处有些方向的曲率是小于 0 的，就可以判定这个点就是鞍点。

从上面的分析不难看出，对于普通的梯度下降优化器，可能会陷入鞍点，但如果利用了二阶信息来梯度下降，就不会陷入鞍点，即在鞍点的时候，当朝着黑塞矩阵负的特征值对应的特征向量的方向更新参数时，损失就会减小，所以可以断定牛顿法（利用二阶信息的梯度下降）可以避免陷入鞍点，但牛顿法计算黑塞矩阵特征值特性向量复杂度太大，一般改进牛顿法，使得在找到近似的负的特征值对应的特征向量的方向的情况下，计算复杂度大大小于计算黑塞矩阵的复杂度。

下面就只剩下了局部最小值无法解决，下面一句话非常让人出乎预料但思考一下又感觉非常神奇：

******在某个维度是局部最小值的点，他在更高的维度中可能是鞍点。******

所以说，在低维空间中中没有路可以走，但在高维空间中可能就有路可以走了。

下图是一个实验证明：

五、训练技巧：Batch

在每一个 epoch 之前，在分 batch 前都会进行 shuffle ，即每一个 epoch 的 batches 都不一样。

这部分注意讨论：小 batches 和大 batches 对训练的影响。

对于大 batches ，蓄力比较长，每次更新更靠谱；对于小 batches ，更新的次数比较多，每次更新的 noisy 比较大。表面上看，大 batches 更新一次，一次所需的时间比较长，小 batches，更新20次，更新一次的时间比较短。那两种的总和时间怎么样呢？

实际上，由于GPU的并行运算，对于一个 batches ，无论是一个样本还是20个样本所用的时间几乎一样，这就导致了小 batches 由于更新次数比较多，它所需的训练时长会大的多。但GPU运算也并不是每个 batches 不论多大时间都一样，一个 batch 所需的时间和 batch 的大小的关系如下（在MNIST数据集上的示例）：

可以看出一个长为1到1000的 batch 所需的时间变化很小，但GPU的并行通道也有其容限，当batch 更大时，所需时间也会随之相应增大。

从上面的分析可知，对于一个任务，batch 的大小如果很小，它的训练时间会很长，增大 batch 时由于迭代次数的下降会使得训练时间大大减小。

下面是一个任务的一个完整的 epoch 所需的时间和 batch size 的关系：

从上面的分析可知，在明显训练时，大的 batch 就一定好吗？其实不然，训练时间并不是评判模型好坏的唯一标准，如果小的 batch 可以使没模型的性能更好的话，那么选用多大的 batch 还是模型训练时的一个值得考量的因素。其实事实就是这样的，batch 的大小确实影响模型的性能，小的 batch ，即 noisy 的梯度会使得模型的性能更好，下面的两幅图是在 train set 上的实验测试结果：

可见对于小的 batch ，模型的正确率更高。

怎么解释呢？对于full batch ，当梯度下降到梯度为 0 的地方时，容易停滞，不再优化，但当使用小 batch 时，由于梯度是 noisy 的，优化过程不容易陷入停滞。

上面说明了小的 batch 对 train accuracy比较好，但其实小的 batch 对 test accuracy 也比较好，

下面是一些实验的结果：

从实验结果来看，Small batch 和 Large batch 使 train accuracy 相等时，在测试集上， Large batch可能会出现 overfitting ，原因是什么呢？

下面是一个解释：

下图代表损失函数的图像，有两个Local minima（局部极小值），大小几乎一样，即在训练集上的精度一样，但一个是比较胖的谷（Flat Minima），一个是比较瘦的谷（Sharp Minima）：

但 Large batch 会比较稳定地向一个Local minima 前进，会稳定地进入一个 Local minima ，就不会出来了（可能是上面两个中地任何一个），但 Small batch 如果进入 Sharp Minima，它由于有噪声的存在，它可能会跳出来，但当它进入 Flat Minima 时，即使有小的噪声存在，它跳出来的可能性也比较小。

即从上面的分析可知，Large batch 相对于 Small batch 更容易进入 Sharp Minima，而 Small batch更容易进入 Flat Minima 。

但 train data 和 test data 肯定是不一样的，肯定是有一点误差的，即 train loss 和 test loss 的图像可能是如下：

可以明显地看出 Flat Minima 的 test loss 是明显小于 Sharp Minima 的，所以可以说 Flat Minima是比 Sharp Minima 更好的 Minima 。

以上就解释了为什么 Small batch 对 test accuracy更好，而 Large batch不好（容易在测试集上overfitting）

总结一下：

Large batch 在训练时间上有优势，但在优化效果（train accuracy）和泛化效果（test accuracy）上 Small batch 更有优势。

六、梯度下降法的优化

之前写过这部分相关的文章，点这里

梯度项优化：希望越过局部极小值

动量法：添加积分项，累积过去的梯度

Nesterov：添加微分项，预测未来的梯度

学习率项优化

问题：

当 train loss 不再下降时，不一定就一定是临界点，也可能是学习率过大：

当两个维度的范围不一样时，即在梯度下降过程中一个维度梯度大，一个维度梯度小，无论让学习率变大还是变小都会出现问题：

要想解决上面的问题，一个解决方法是不同的维度要用不同的学习率：

AdaGrad优化法：在梯度较小的维度上进行自适应放大，在梯度较大的维度上进行自适应缩小。该方法同一个维度的学习率只会逐渐减小（弊端）。

RMSprop优化法：将累积的比较久远的梯度对后续的影响降低。解决了 AdaGrad 的弊端。

梯度和学习率一起优化

Adam优化法：RMSprop + 动量法

同样是上面图中的优化，使用Adam的效果为：

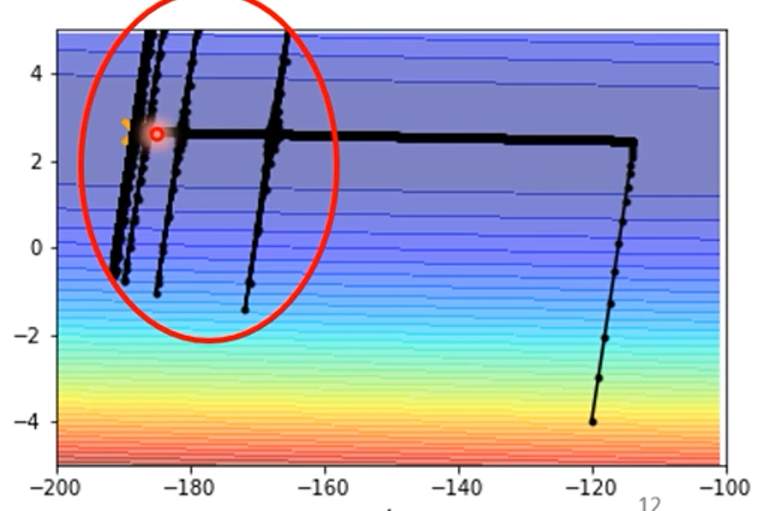
可见，在上下维度出现了跳动，是因为在上下的维度上的梯度太小了，但又在一直更新，上下维度的学习率变得很大，出现了跳动，但即使上下维度上跳出去，跳到了梯度大的地方，学习率又会减小，还是会回来的。

如何解决上面的问题？

一种方法是： Learning Rate Scheduling ，

即让 $\eta$ 随时间t逐渐变小：

结果可解决震荡，为：

另一种方法是：Warm Up（在 bert 中常用）

即让 $\eta$ 随时间 t 先变大后变小。初始的时候让 $\eta$ 很小，即不让参数开始的时候走的太远，让参数在初始的地方做一些探索，搜集一些有关的情报。

对Warm Up 更详细的介绍在论文：点这里

上面的所有有关优化的技巧都是在崎岖的山路上找到新的路，来让优化过程更有效，下面一个方法并不上向上面的那样，而是直接改变崎岖的山路，然山路变得不崎岖，从而更容易地优化，这个方法就是 batch normalization ，关于batch normalization，之前写过的文章中有，点这里